题目内容
11.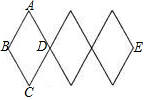 如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )
如图,是伸缩衣架的实物图和示意图,它是由4条短木棒和4条长木棒组成的三个全等的菱形,其中AB=20cm,当∠BAD由60°变为120°时,衣架的总长度BE拉长了( )| A. | (20$\sqrt{3}$-20)cm | B. | (40$\sqrt{3}$-40)cm | C. | (60-30$\sqrt{3}$)cm | D. | (60$\sqrt{3}$-60)cm |
分析 根据菱形的性质分别得出∠BAD由60°变为120°前后BE的长,进而得出答案.
解答 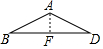 解:当∠BAD=60°时,连接BD,
解:当∠BAD=60°时,连接BD,
∵四边形ABCD是菱形,则AB=AD,
∴△ABD是等边三角形,
∴AB=BD=20cm,
如图所示:过点A作AF⊥BD于点F,
∵∠BAD=120°,
∴∠BAF=60°,
则∠B=30°,
故BF=ABcos30°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$(cm),
则BD=20$\sqrt{3}$cm,
可得衣架的总长度BE拉长了:3×20$\sqrt{3}$-3×20=60$\sqrt{3}$-60.
故选:D.
点评 此题主要考查了菱形的性质以及锐角三角函数关系,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
1.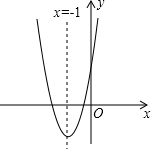 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
①b2=4ac;②abc>0;③a>c;④4a-2b+c>0,其中正确的个数有( )
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,给出下列结论:①b2=4ac;②abc>0;③a>c;④4a-2b+c>0,其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.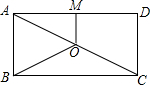 如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
 如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )
如图,点O是矩形ABCD的对角线AC的中点,OM∥AB交AD于点M,若OM=3,BC=10,则OB的长为( )| A. | 5 | B. | 4 | C. | $\frac{\sqrt{34}}{2}$ | D. | $\sqrt{34}$ |
19.若α、β为方程2x2-5x-1=0的两个实数根,则2α2+3αβ+5β的值为( )
| A. | -13 | B. | 12 | C. | 14 | D. | 15 |
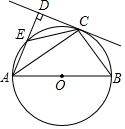 如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB. 如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )
如图所示的几何体是由一个长方体和一个圆柱体组成的,则它的主视图是( )


