题目内容
10.(1)解方程:4y-3(2+y)=5-2(1-2y)(2)解方程:$x-\frac{1-x}{3}=\frac{x+2}{6}-1$.
分析 (1)先去括号,再移项、合并同类项,把x的系数化为1即可;
(2)先去分母,再去括号,再移项、合并同类项,把x的系数化为1即可.
解答 解:(1)去括号得,4y-6-3y=5-2+4y,
移项得,4y-3y-4y=5-2+6,
合并同类项得,-3y=9,
系数化为1得,y=-3;
(2)去分母得,6x-2(1-x)=x+2-6,
去括号得,6x-2+2x=x+2-6,
移项得,6x+2x-x=2-6+2,
合并同类项得,7x=-2,
x的系数化为1得,x=-$\frac{2}{7}$.
点评 本题考查的是解一元一次方程,熟知去分母、去括号、移项、合并同类项、系数化为1是解一元一次方程的一般步骤是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.某养殖户的养殖成本逐年增长,已知第一年的养殖成本为12万元,第3年的养殖成本为17万元.设每年平均增长的百分率为x,则下面所列方程中正确的是( )
| A. | 12(1-x)2=17 | B. | 17(1-x)2=12 | C. | 17(1+x)2=12 | D. | 12(1+x)2=17 |
1. 如图,若∠1=∠2=∠3,则图中的相似三角形有( )
如图,若∠1=∠2=∠3,则图中的相似三角形有( )
 如图,若∠1=∠2=∠3,则图中的相似三角形有( )
如图,若∠1=∠2=∠3,则图中的相似三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
18.一架a米长的梯子斜靠在墙上,测得它与地面夹角为θ,则梯子底端到墙的距离为( )
| A. | asinθ | B. | acosθ | C. | $\frac{a}{tanθ}$ | D. | $\frac{a}{cosθ}$ |
19.方程4x2-3x+1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
20.已知y是x的一次函数,下表列出了部分对应值,则n=3.
| x | -2 | 0 | 1 |
| y | -3 | 1 | n |
 如图所示,过六边形的顶点A的所有对角线可将六边形分成4个三角形.
如图所示,过六边形的顶点A的所有对角线可将六边形分成4个三角形.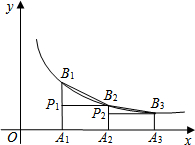 如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=$\frac{1}{x}$(x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+S20=$\frac{10}{21}$.
如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An-1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=$\frac{1}{x}$(x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+S20=$\frac{10}{21}$.