题目内容
13．
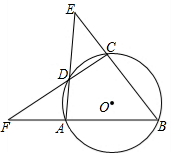如图，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，∠DCE=80°，∠F=25°，则∠E的度数为（ ）| A． | 55° | B． | 50° | C． | 45° | D． | 40° |
分析 根据三角形的外角的性质求出∠B，根据圆内接四边形的性质和三角形内角和定理计算即可．
解答 解：∠B=∠DCE-∠F=55°，
∵四边形ABCD是⊙O的内接四边形，
∴∠EDC=∠B=55°，
∴∠E=180°-∠DCE-∠EDC=45°，
故选：C．
点评 本题考查的是圆内接四边形的性质和三角形内角和定理，掌握圆内接四边形的任意一个外角等于它的内对角是解题的关键．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
3．若两个有理数的和等于0，则这两个有理数（ ）
| A． | 都是0 | B． | 有一个为0 | C． | 一定是一正一负 | D． | 互为相反数 |
4．用配方法解方程x2-2x-1=0，原方程应变形为（ ）
| A． | （x-1）2=2 | B． | （x+1）2=2 | C． | （x-1）2=1 | D． | （x+1）2=1 |
8．-$\sqrt{3}$的绝对值是（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | -$\frac{\sqrt{3}}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{1}{3}$ |
5．样本数据3，2，4，a，8的平均数是4，则这组数据的众数是（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 8 |
2．下列实数中，有理数是（ ）
| A． | $\root{3}{4}$ | B． | $\frac{π}{2}$ | C． | $\sqrt{8}$ | D． | 3.14159 |