题目内容
已知x1,x2(x1<x2)是二次方程x2-(m-1)x+n=0的两个实数根,y1,y2是二次方程y2+(n+1)y-6m=0的两个实数根,且x1-y1=2,y2-x2=2,求m,n的值.
考点:根与系数的关系
专题:
分析:首先由根与系数的关系,得出x1+x2=m-1,x1x2=n,y1+y2=n+1,y1y2=-6m,进一步利用已知条件与原方程之间的联系,整理探讨得出答案即可.
解答:解:∵x1,x2(x1<x2)是二次方程x2-(m-1)x+n=0③的两个实数根,y1,y2是二次方程y2+(n+1)y-6m=0⑤的两个实数根,
∴x1+x2=m-1,x1x2=n,△=(m-1)2-4n>0,
y1+y2=-(n+1),y1y2=-6m,
又∵x1-y1=2,①
y2-x2=2,②
①-②,得x1+x2-(y1+y2)=0,
m-1+(n+1)=0,
m+n=2,
m=2-n④,
④代入③,得x2-(2-n-1)x+n=0
x2-(1-n)x+n=0
得(x-n)(x-1)=0
x1=n,x2=1或x1=1,x2=n,
验增根:假如x2=1代入②,得y2=3,
再把y2=3代入⑤,得9-3(n+1)-6m=0
3n+6m=6,
n+2m=2,
因为m=n+2,得n=-
,m=
,
因为x1<x2,
所以n=-
,m=
,
假如x1=1代入①,得y1=-1,
再把y1=-1代入⑤,得1+(n+1)-6m=0
n-6m=-2
因为m=n+2,得n=-2,m=0
因为x1<x2,
所以n=-2,m=0为增根
所以n=-
,m=
.
∴x1+x2=m-1,x1x2=n,△=(m-1)2-4n>0,
y1+y2=-(n+1),y1y2=-6m,
又∵x1-y1=2,①
y2-x2=2,②
①-②,得x1+x2-(y1+y2)=0,
m-1+(n+1)=0,
m+n=2,
m=2-n④,
④代入③,得x2-(2-n-1)x+n=0
x2-(1-n)x+n=0
得(x-n)(x-1)=0
x1=n,x2=1或x1=1,x2=n,
验增根:假如x2=1代入②,得y2=3,
再把y2=3代入⑤,得9-3(n+1)-6m=0
3n+6m=6,
n+2m=2,
因为m=n+2,得n=-
| 2 |
| 3 |
| 4 |
| 3 |
因为x1<x2,
所以n=-
| 2 |
| 3 |
| 4 |
| 3 |
假如x1=1代入①,得y1=-1,
再把y1=-1代入⑤,得1+(n+1)-6m=0
n-6m=-2
因为m=n+2,得n=-2,m=0
因为x1<x2,
所以n=-2,m=0为增根
所以n=-
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查了一元二次方程根与系数的关系,方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
下列方程组中,是二元一次方程组的为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
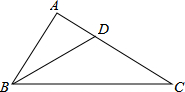 已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.
已知,如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,交AC于点D,求证:点D在BC的垂直平分线上.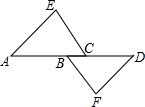 如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.
如图,已知△ACE≌△DBF,点A、B、C、D在同一条直线上,AE=DF,CE=BF,AD=8,BC=2.