Question

3．如图，在直角坐标系中，正方形OABC的顶点O与原点重合，顶点A，C分别在x轴，y轴上，反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象与正方形的两边AB，BC分别交于点M，N，ND⊥x轴，垂足为D，连结OM，ON，MN，下列结论：①△OCN≌△OAM；②MN=CN+AM；③四边形DAMN与△MON面积相等；④若∠MON=45°，MN=4，则点C的坐标为（0，2$\sqrt{2}$+2），其中正确结论的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 根据反比例函数的比例系数的几何意义得到S_△ONC=S_△OAM=$\frac{1}{2}$k，即$\frac{1}{2}$OC•NC=$\frac{1}{2}$OA•AM，而OC=OA，则NC=AM，由SAS得出△OCN≌△OAM，①正确；
根据全等的性质得到ON=OM，由于k的值不能确定，则∠MON的值不能确定，无法确定△ONM为等边三角形，得出②错误；
根据S_△OND=S_△OAM=$\frac{1}{2}$k和S_△OND+S_{四边形DAMN}=S_△OAM+S_△OMN，即可得到S_{四边形DAMN}=S_△OMN；③正确；
作NE⊥OM于E点，则△ONE为等腰直角三角形，设NE=x，则OM=ON=$\sqrt{2}$x，EM=$\sqrt{2}$x-x=（$\sqrt{2}$-1）x，在Rt△NEM中，利用勾股定理可求出x²=8+4$\sqrt{2}$，所以ON²=（$\sqrt{2}$x）²=16+8$\sqrt{2}$，易得△BMN为等腰直角三角形，得到BN=$\frac{\sqrt{2}}{2}$MN=2$\sqrt{2}$，设正方形ABCO的边长为a，在Rt△OCN中，利用勾股定理可求出a的值为2$\sqrt{2}$+2，从而得到C点坐标，④正确；即可得出结论．

解答 解：∵点M、N都在y=$\frac{k}{x}$的图象上，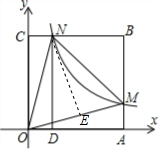
∴S_△ONC=S_△OAM=$\frac{1}{2}$k，即$\frac{1}{2}$OC•NC=$\frac{1}{2}$OA•AM，
∵四边形ABCO为正方形，
∴OC=OA，∠OCN=∠OAM=90°，
∴NC=AM，
在△OCN和△OAM中，$\left\{\begin{array}{l}{OC=OA}&{\;}\\{∠OCN=∠OAM}&{\;}\\{CN=AM}&{\;}\end{array}\right.$，
∴△OCN≌△OAM（SAS），①正确；
∴ON=OM，
∵k的值不能确定，
∴∠MON的值不能确定，
∴△ONM只能为等腰三角形，不能确定为等边三角形，
∴ON≠MN，
∴MN≠CN+AM；②错误；
∵S_△OND=S_△OAM=$\frac{1}{2}$k，
而S_△OND+S_{四边形DAMN}=S_△OAM+S_△OMN，
∴四边形DAMN与△MON面积相等，③正确；
作NE⊥OM于E点，如图，
∵∠MON=45°，
∴△ONE为等腰直角三角形，
∴NE=OE，设NE=x，则ON=$\sqrt{2}$x，
∴OM=$\sqrt{2}$x，
∴EM=$\sqrt{2}$x-x=（$\sqrt{2}$-1）x，
在Rt△NEM中，MN=4，
∵MN²=NE²+EM²，即4²=x²+[（$\sqrt{2}$-1）x]²，
∴x²=8+4$\sqrt{2}$，
∴ON²=（$\sqrt{2}$x）²=16+8$\sqrt{2}$，
∵CN=AM，CB=AB，
∴BN=BM，
∴△BMN为等腰直角三角形，
∴BN=$\frac{\sqrt{2}}{2}$MN=2$\sqrt{2}$，
设正方形ABCO的边长为a，则OC=a，CN=a-2$\sqrt{2}$，
在Rt△OCN中，∵OC²+CN²=ON²，
∴a²+（a-2$\sqrt{2}$）²=16+8$\sqrt{2}$，
解得a₁=2$\sqrt{2}$+2，a₂=-2（舍去），
∴OC=2$\sqrt{2}$+2，
∴C点坐标为（0，2$\sqrt{2}$+2），④正确．
正确结论的个数是3个，故选：C．

点评 本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、比例系数的几何意义和正方形的性质；熟练运用勾股定理和等腰直角三角形的性质进行几何计算．