题目内容
3. 如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD=45°.
如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD=45°.
分析 由翻折的性质可知∠AFE=∠EFD,在Rt△EDC中,由三角形内角和求解即可.
解答 解:由翻折的性质可知;∠AFE=∠EFD.
∵△ABC为等边三角形,
∴∠B=60°,∠C=60°,∠A=∠EDF=60°.
∵ED⊥BC,
∴△EDC为直角三角形,
∴∠FDB=30°,
∴∠AFE+∠EFD=60°+30°=90°,
∴∠EFD=45°.
故答案为:45°
点评 本题主要考查是翻折的性质,关键是根据等边三角形的性质和翻折的性质解答.

练习册系列答案
相关题目
11.等腰三角形的一个角是70°,则它的底角是( )
| A. | 70° | B. | 70°或55° | C. | 80°和100° | D. | 110° |
8.下列代数式一定表示正数的是( )
| A. | 2a | B. | a+9 | C. | a2+1 | D. | |a+1| |
15.下列结论中错误的是( )
| A. | 三角形的内角和等于180° | |
| B. | 三角形的外角和小于四边形的外角和 | |
| C. | 五边形的内角和等于540° | |
| D. | 正六边形的一个内角等于120° |
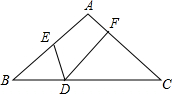 如图:在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.求证:BD•CD=BE•CF.
如图:在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.求证:BD•CD=BE•CF. 已知如图直线y=2x+1与直线y=kx+6交于点P(2,5).
已知如图直线y=2x+1与直线y=kx+6交于点P(2,5).