Question

12．已知Rt△ABC中，AB=10，AC=BC，∠ACB=90°，点D是Rt△ABC的外接圆上一点，且AD=8，则线段CD的长为$\sqrt{2}$或7$\sqrt{2}$．

Answer 1

分析 分两种情况：
①当C与D在直径AB的两侧时，如图1，作辅助线，构建直角三角形，利用勾股定理分别计算CE和DE的长，并相加得CD的长为7$\sqrt{2}$；
②当D与C在直径AB的同侧时，如图2，作辅助线，构建直角三角形，利用勾股定理列方程求出CD的长．

解答 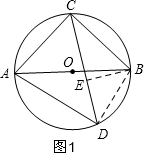解：分两种情况：
①当C与D在直径AB的两侧时，如图1，
过B作BE⊥CD于E，连接BD，
∵AC=BC，∠ACB=90°，
∴△ABC是等腰直角三角形，
∴∠CAB=∠CBA=45°，
∵AB=10，
∴BC=$\frac{10}{\sqrt{2}}$=5$\sqrt{2}$，
∵AB是⊙O的直径，
∴∠ADB=90°，
∵AD=8，
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6，
∵∠CDB=∠CAB=45°，
∴△BED是等腰直角三角形，
∴BE=ED=$\frac{6}{\sqrt{2}}$=3$\sqrt{2}$，
由勾股定理得：CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\sqrt{（5\sqrt{2}）^{2}-（3\sqrt{2}）^{2}}$=4$\sqrt{2}$，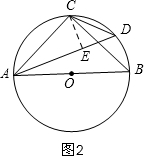
∴CD=CE+ED=7$\sqrt{2}$，
②当D与C在直径AB的同侧时，如图2，
过C作CE⊥AD于E，
则∠CDA=∠CBA=45°，
设DE=CE=x，则AE=8-x，CD=$\sqrt{2}$x，
由勾股定理得：AC²=AE²+CE²，
（5$\sqrt{2}$）²=x²+（8-x）²，
解得：x=1或7，
当x=1时，CD=$\sqrt{2}$，
当x=7时，CD=7$\sqrt{2}$（舍），
综上所述，CD=$\sqrt{2}$或7$\sqrt{2}$，
故答案为：$\sqrt{2}$或7$\sqrt{2}$．

点评 本题是直角三角形的外接圆，考查了直角三角形外接圆的性质和圆周角定理，恰当地作垂线段，构建等腰直角三角形是关键，利用勾股定理列等式或方程求解此题．