题目内容
6.下列说法中正确的是( )| A. | 正数和负数统称有理数 | B. | 若|a|=|b|,则a=b. | ||
| C. | -0.210×510=(-0.2×5)10=1 | D. | x是有理数,则x2+1永远是正数 |
分析 根据有理数的分类即可判断选项A;根据绝对值的性质判断选项B;根据积的立方的逆运算即可判断选项C;根据非负数的性质即可判断选项D.
解答 解:A、正数和负数和0统称有理数,故选项错误;
B、若|a|=|b|,则a=±b,故选项错误;
C、-0.210×510=-(0.2×5)10=-1,故选项错误;
D、x是有理数,则x2+1≥1,永远是正数,故选项正确.
故选:D.
点评 考查了有理数的分类,绝对值的性质,积的立方的逆运算,非负数的性质,综合性较强,难度一般.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
16.下列说法中,不正确是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边平行另一组对边相等的四边形是平行四边形 |
17.一件工作甲单独做a小时完成,乙单独做b小时完成,甲、乙两人一起完成这项工作需要的小时数是( )
| A. | $\frac{ab}{a+b}$ | B. | $\frac{1}{a+b}$ | C. | $\frac{1}{a}$+$\frac{1}{b}$ | D. | $\frac{1}{ab}$ |
15.已知甲、乙、丙三个数,甲=5+$\sqrt{13}$,乙=2+$\sqrt{19}$,且甲>丙>乙,则下列符合条件的丙是( )
| A. | 1+$\sqrt{23}$ | B. | 4+$\sqrt{26}$ | C. | 4+$\sqrt{15}$ | D. | 4+$\sqrt{3}$ |
 计算或化简求值.
计算或化简求值.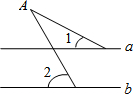 如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.
如图,已知直线a∥b,∠1=28°,∠2=52°,那么∠A的度数是24°.