题目内容
17.有两个一元二次方程M:ax2+bx+c=0;N:cx2+bx+a=0,其中ac≠0,a≠c.下列四个结论中:正确的个数有( )①如果方程M有两个相等的实数根,那么方程N也有两个相等的实数根;
②如果ac<0,方程M、N都有两个不相等的实数根;
③如果2是方程M的一个根,那么$\frac{1}{2}$是方程N的一个根;
④如果方程M和方程N有一个相同的根,那么这个根必是x=1.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 ①方程ax2+bx+c=0有两个相等的实数根,则△=b2-4ac=0,对于方程cx2+bx+a=0,△=b2-4ac=0,则方程N也有两个相等的实数根;
②利用ac<0和根的判别式进行判断即可;
③把x=2代入ax2+bx+c=0得:4a+2b+c=0,等式的两边通除以4得到$\frac{1}{4}$c+$\frac{1}{2}$b+a=0,于是得到结论正确;
④如果方程M和方程N有一个相同的根,那么这个根可能是x=±1.
解答 解:①∵方程M有两个相等的实数根,∴△=b2-4ac=0,
∵方程N的△=b2-4ac=0,∴方程N也有两个相等的实数根,故正确;
②∵ac<0,∴b2-4ac>0,∴程M、N都有两个不相等的实数根;故正确;
③∵把x=2代入ax2+bx+c=0得:4a+2b+c=0,
∴$\frac{1}{4}$c+$\frac{1}{2}$b+a=0,∴$\frac{1}{2}$是方程N的一个根;故正确;
④如果方程M和方程N有一个相同的根,那么这个根可能是x=±1;故错误.
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
5.若一组数据1,2,x,4的众数是1,则这组数据的方差为( )
| A. | 1 | B. | 2 | C. | 1.5 | D. | $\sqrt{2}$ |
2.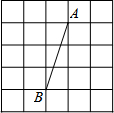 如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
 如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )
如图,正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数有( )| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
6.已知:⊙O的直径等于4,点P到圆心O的长度OP=4,则点P与⊙O的位置关系为( )
| A. | P在⊙O上 | B. | P在⊙O内 | C. | P在⊙O外 | D. | 不确定 |
 电子跳蚤游戏盘为△ABC,AB=8,AC=9,BC=10,如果电子跳蚤开始时在BC边上的P0点,BP0=4.第一步跳蚤跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2 跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第2015次落点为P2016,则P3与P2016之间的距离为1.
电子跳蚤游戏盘为△ABC,AB=8,AC=9,BC=10,如果电子跳蚤开始时在BC边上的P0点,BP0=4.第一步跳蚤跳到AC边上P1点,且CP1=CP0;第二步跳蚤从P1跳到AB边上P2点,且AP2=AP1;第三步跳蚤从P2 跳回到BC边上P3点,且BP3=BP2;…跳蚤按上述规则跳下去,第2015次落点为P2016,则P3与P2016之间的距离为1. 如图,点B、C、D在同一直线上,AB=AD=CD,∠C=35°.求∠BAD的度数.
如图,点B、C、D在同一直线上,AB=AD=CD,∠C=35°.求∠BAD的度数.