题目内容
2．
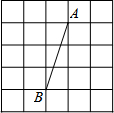如图，正方形网格中，网格线的交点称为格点，已知A、B是两格点，如果C也是图中的格点，且使得△ABC为等腰三角形，则点C的个数有（ ）| A． | 4个 | B． | 6个 | C． | 8个 | D． | 10个 |
分析 根据AB的长度确定C点的不同位置，由已知条件，利用勾股定理可知AB=$\sqrt{10}$，然后即可确定C点的位置．
解答 
解：如图，AB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
∴当△ABC为等腰三角形，则点C的个数有8个，
故选C．
点评 本题考查了等腰三角形的判定，熟练掌握等腰三角形的判定定理是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
12．
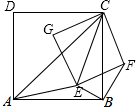如图，已知AC，EC分别为正方形ABCD和正方形EFCG的对角线，点E在△ABC内，连接BF，∠CAE+∠CBE=90°．
（1）求证：△CAE∽△CBF；
（2）若BE=1，AE=2，求CE的长．
如图，已知AC，EC分别为正方形ABCD和正方形EFCG的对角线，点E在△ABC内，连接BF，∠CAE+∠CBE=90°．（1）求证：△CAE∽△CBF；
（2）若BE=1，AE=2，求CE的长．
14．Rt△ABC中，∠C=90°，AC=3，BC=4，则中线CD的长是（ ）
| A． | 2 | B． | 2.5 | C． | 5 | D． | 1.5 |