题目内容
19.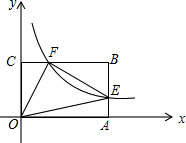 如图,在直角坐标系中,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边AB、BC分别交于E、F,AB=nAE(n≥2),m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$.
如图,在直角坐标系中,双曲线y=$\frac{2}{x}$(x>0)与矩形OABC的边AB、BC分别交于E、F,AB=nAE(n≥2),m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$.(1)当n=2时,S矩形OABC=4,S△BEF=$\frac{1}{2}$、S△OEF=$\frac{3}{2}$;
(2)求m关于n的函数关系式,并求m的最小值;
(3)当m=$\frac{3}{5}$且△OEF为直角三角形时,求OA的长.
分析 (1)由n=2时,可设E的坐标为:(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{4}{x}$),F的坐标为($\frac{x}{2}$,$\frac{4}{x}$),继而求得答案;
(2)首先设点E的坐标为(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{2n}{x}$),点F的坐标为:($\frac{x}{n}$,$\frac{2n}{x}$),然后分别求得△BEF与△OEF的面积,继而求得答案;
(3)首先由m=$\frac{3}{5}$,求得n=4,再设点E的坐标为(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{2n}{x}$),点F的坐标为:($\frac{x}{n}$,$\frac{2n}{x}$),再由△OEF为直角三角形,利用勾股定理即可求得答案.
解答 解:(1)∵n=2,
∴AB=2AE,
设E的坐标为:(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{4}{x}$),F的坐标为($\frac{x}{2}$,$\frac{4}{x}$),
∴S矩形OABC=OA•AB=x•$\frac{4}{x}$=4,S△BEF=$\frac{1}{2}$BE•BF=$\frac{1}{2}$×$\frac{2}{x}$×(x-$\frac{x}{2}$)=$\frac{1}{2}$,
∴S△OEF=S矩形OABC-S△BEF-S△OAE-S△OCF=4-$\frac{1}{2}$-1-1=$\frac{3}{2}$;
故答案为:4,$\frac{1}{2}$,$\frac{3}{2}$;
(2)∵AB=nAE(n≥2),
∴设点E的坐标为(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{2n}{x}$),点F的坐标为:($\frac{x}{n}$,$\frac{2n}{x}$),
∴S△BEF=$\frac{1}{2}$BE•BF=$\frac{1}{2}$×$\frac{2n-2}{x}$×(x-$\frac{x}{n}$)=$\frac{(n-1)^{2}}{n}$,
∴S△OEF=S矩形OABC-S△BEF-S△OAE-S△OCF=2n-$\frac{(n-1)^{2}}{n}$-1-1=$\frac{{n}^{2}-1}{n}$,
∴m=$\frac{{S}_{△BEF}}{{S}_{△OEF}}$=$\frac{(n-1)^{2}}{{n}^{2}-1}$=$\frac{n-1}{n+1}$=1-$\frac{2}{n+1}$≤1,
∴m=$\frac{n-1}{n+1}$,m的最小值为1;
(3)当m=$\frac{3}{5}$时,$\frac{n-1}{n+1}$=$\frac{3}{5}$,解得:n=4;
设点E的坐标为(x,$\frac{2}{x}$),则B的坐标为:(x,$\frac{8}{x}$),点F的坐标为:($\frac{x}{4}$,$\frac{8}{x}$),
∴OF2=($\frac{x}{4}$)2+($\frac{8}{x}$)2,OE2=x2+($\frac{2}{x}$)2,EF2=(x-$\frac{x}{4}$)2+($\frac{6}{x}$)2,
∵△OEF为直角三角形,
∴OF2+EF2=OE2,
∴($\frac{x}{4}$)2+($\frac{8}{x}$)2+(x-$\frac{x}{4}$)2+($\frac{6}{x}$)2=x2+($\frac{2}{x}$)2,
解得:x=4,
∴OA=4.
点评 此题属于反比例函数综合题.考查了反比例函数的k的几何意义以及矩形的面积等知识.注意利用方程思想求解是解此题的关键.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 1 | B. | -1 | C. | 4025 | D. | -4025 |
 如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为3.
如图,在平面直角坐标系中,点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,点C在x轴上.若四边形OABC为平行四边形,则△OBC的面积为3.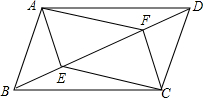 如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:∠EAF=∠FCE.
如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF,FA.求证:∠EAF=∠FCE.