题目内容
12. 已知:如图,△ABC的顶点都在⊙O上,点P在⊙O上,且∠APC=∠CPB=60°.求证:△ABC是等边三角形.
已知:如图,△ABC的顶点都在⊙O上,点P在⊙O上,且∠APC=∠CPB=60°.求证:△ABC是等边三角形.
分析 根据在同圆或等圆中,相等的圆周角所对的弦相等,圆内接四边形对角互补可以证明结论成立.
解答 证明:∵在⊙O中,∠APC=∠CPB=60°,
∴AC=BC,∠APB=120°,
∵四边形APBC是圆内接四边形,
∴∠APB+∠ACB=180°,
∴∠ACB=60°,
∴△ABC是等边三角形.
点评 本题考查圆周角定理、等边三角形的判定,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知a,b互为相反数,则下列各组数中不是互为相反数的是( )
| A. | -2a和-2b | B. | 2a和2b | C. | a+1和b+1 | D. | a+1和b-1 |
4.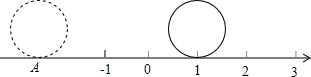 如图,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是 .若点B表示-3.14,则点B在点A的 边(B与点A位置关系)( )
如图,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是 .若点B表示-3.14,则点B在点A的 边(B与点A位置关系)( )
 如图,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是 .若点B表示-3.14,则点B在点A的 边(B与点A位置关系)( )
如图,直径为单位1的圆从原点沿着数轴无滑动的逆时针滚动一周到达A点,则A点表示的数是 .若点B表示-3.14,则点B在点A的 边(B与点A位置关系)( )| A. | π、左 | B. | -π、右 | C. | -π、重合 | D. | D、 |
 已知:如图,AB∥CD,AB=CD,求证:AD∥BC.
已知:如图,AB∥CD,AB=CD,求证:AD∥BC.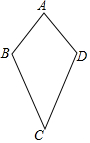 如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( )
如图所示,已知AB=AD,CB=CD,则在以下各结论中,正确的结论为( ) 如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.
如图,已知△ABE≌△ADC,∠1=36°,∠DAE=76°,∠B=25°.求∠DAC、∠C的度数.