题目内容
⊙O中,弦MN把⊙O分成两条弧,它们的度数比为4:5,如果T为MN中点,则∠TMO= ,则弦MN所对的圆周角为 .
考点:圆周角定理,圆心角、弧、弦的关系
专题:计算题
分析:∠MAN与∠MBN为弦MN所对的圆周角,连结ON,如图,根据圆周角定理,由弧MAN与弧MBN的度数比为4:5得到∠MAN与∠MBN的比为4:5,根据圆内接四边形的性质得∠MBN+∠MAN=180°,则可计算出∠MAN=80°,∠MBN=100°;然后根据圆周角定理得到∠MON=2∠MAN=160°,再利用三角形的内角和定理计算∠TMO.
解答:解:如图, ∠MAN与∠MBN为弦MN所对的圆周角,连结ON,
∠MAN与∠MBN为弦MN所对的圆周角,连结ON,
∵弧MAN与弧MBN的度数比为4:5,
∴∠MAN与∠MBN的比为4:5,
而∠MBN+∠MAN=180°,
∴∠MAN=
×180°=80°,∠MBN=
×180°=100°;
∵∠MON=2∠MAN=160°,
∴∠TMO=
(180°-160°)=10°.
故答案围殴10°,80°或100°.
 ∠MAN与∠MBN为弦MN所对的圆周角,连结ON,
∠MAN与∠MBN为弦MN所对的圆周角,连结ON,∵弧MAN与弧MBN的度数比为4:5,
∴∠MAN与∠MBN的比为4:5,
而∠MBN+∠MAN=180°,
∴∠MAN=
| 4 |
| 9 |
| 5 |
| 9 |
∵∠MON=2∠MAN=160°,
∴∠TMO=
| 1 |
| 2 |
故答案围殴10°,80°或100°.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

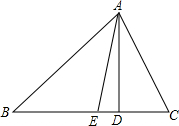 如图,在△ABC中,AD⊥BC,AE平分∠BAC,交BC于点E.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,交BC于点E.