题目内容
若点A(0,1),点B(-1,3)和点C(2,x+1)在同一条直线上,则x的值为 .
考点:一次函数图象上点的坐标特征
专题:
分析:先用待定系数法求出直线AB的解析式,再把点C(2,x+1)代入求出x的值即可.
解答:解:设直线AB的解析式为y=kx+b(k≠0),
∵点A(0,1),点B(-1,3),
∴
,解得
,
∴直线AB的解析式为y=-2x+1,
∵点C(2,x+1)在直线上,
∴x+1=-4+1,解得x=-4.
故答案为:-4.
∵点A(0,1),点B(-1,3),
∴
|
|
∴直线AB的解析式为y=-2x+1,
∵点C(2,x+1)在直线上,
∴x+1=-4+1,解得x=-4.
故答案为:-4.
点评:本题考查的是一次函数图象上点坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目

 如图,等腰梯形ABCD中,点E、F分别是对角线AC、BD的中点,证明:四边形EFBC是等腰梯形.
如图,等腰梯形ABCD中,点E、F分别是对角线AC、BD的中点,证明:四边形EFBC是等腰梯形. 如图,以点O为旋转中心,将线段AB按顺时针方向旋转60°,作出经旋转所得的线段A′B′,并求直线A′B′与直线AB所成的锐角的度数.
如图,以点O为旋转中心,将线段AB按顺时针方向旋转60°,作出经旋转所得的线段A′B′,并求直线A′B′与直线AB所成的锐角的度数. 如图,点E、F分别在平行四边形ABCD的边DC和AB上,且DF∥BE,EF交BD于点O,那么四边形FBED是平行四边形吗?
如图,点E、F分别在平行四边形ABCD的边DC和AB上,且DF∥BE,EF交BD于点O,那么四边形FBED是平行四边形吗?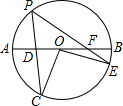 如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=
如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=