题目内容
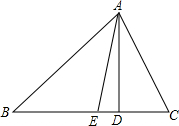 如图,在△ABC中,AD⊥BC,AE平分∠BAC,交BC于点E.
如图,在△ABC中,AD⊥BC,AE平分∠BAC,交BC于点E.(1)∠B=40°,∠C=70°,求∠EAD的大小.
(2)若∠B<∠C,请说明:2∠EAD=∠C-∠B.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=
∠BAC,故∠EAD=∠EAC-∠DAC;
(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
| 1 |
| 2 |
(2)由(1)知,用∠C和∠B表示出∠EAD,即可知2∠EAD与∠C-∠B的关系.
解答:解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°-∠B-∠C=80°.
∵AE是角平分线,
∴∠EAC=
∠BAC=40°.
∵AD是高,∠C=70°,
∴∠DAC=90°-∠C=20°,
∴∠EAD=∠EAC-∠DAC=40°-20°=20°;
(2)由(1)知,∠EAD=∠EAC-∠DAC=
∠BAC-(90°-∠C)①,
把∠BAC=180°-∠B-∠C代入①,
整理得,∠EAD=
∠C-
∠B,
所以2∠EAD=∠C-∠B.
∴∠BAC=180°-∠B-∠C=80°.
∵AE是角平分线,
∴∠EAC=
| 1 |
| 2 |
∵AD是高,∠C=70°,
∴∠DAC=90°-∠C=20°,
∴∠EAD=∠EAC-∠DAC=40°-20°=20°;
(2)由(1)知,∠EAD=∠EAC-∠DAC=
| 1 |
| 2 |
把∠BAC=180°-∠B-∠C代入①,
整理得,∠EAD=
| 1 |
| 2 |
| 1 |
| 2 |
所以2∠EAD=∠C-∠B.
点评:本题考查了三角形内角和定理、角的平分线的性质、直角三角形的性质,结合图形类比得出答案求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列图形中,有三条对称轴的是( )
| A、等腰三角形 | B、五角形 |
| C、等边三角形 | D、正方形 |
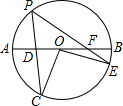 如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=
如图所示,AB是⊙O的直径,弦PC交OA于点D,弦PE交OB于点F,且OC=DC,OF=EF,若∠C=∠PFA,则∠CPE=