题目内容
 如图,⊙O的直径AB=10cm,弦CD⊥AB于E,CD=6cm.求AE的长.
如图,⊙O的直径AB=10cm,弦CD⊥AB于E,CD=6cm.求AE的长.考点:垂径定理,勾股定理
专题:
分析:连接OC.先根据垂径定理求出CE=
CD=3cm,再根据勾股定理求得OE的长,然后根据AE=OA+OE即可求解.
| 1 |
| 2 |
解答: 解:连接OC.
解:连接OC.
∵AB是⊙O的直径弦CD⊥AB于E,CD=6cm,
∴CE=
CD=3cm,
在直角三角形OEC中,∵∠OEC=90°,OC=5cm,CE=3cm,
∴OE=
=4cm,
∴AE=OA+OE=9cm.
 解:连接OC.
解:连接OC.∵AB是⊙O的直径弦CD⊥AB于E,CD=6cm,
∴CE=
| 1 |
| 2 |
在直角三角形OEC中,∵∠OEC=90°,OC=5cm,CE=3cm,
∴OE=
| OC2-CE2 |
∴AE=OA+OE=9cm.
点评:本题主要考查了垂径定理和勾股定理,求出CE=
CD=3cm是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目

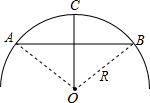 如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径.
如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径.