题目内容
用不同的正多边形瓷砖进行地面铺设，若在一个顶点处铺上一个正三角形和一个正九边形，还需要一个正 边形才能密铺．
考点：平面镶嵌（密铺）
专题：
分析：根据正三角形的每个内角为60°，正九边形的每个内角为140°，若能构成镶嵌，则还需正多边形的每个内角为360°-60°-140°=160°，据此即可求解．
解答：解：∵正三角形的每个内角为180°÷3=60°，
正九边形的每个内角为180°-
=140°，
∴还需正多边形的每个内角为360°-60°-140°=160°，
其每个外角为180°-160°=20°，
其边数为
=18．
故答案为：十八．
正九边形的每个内角为180°-
| 360 |
| 9 |
∴还需正多边形的每个内角为360°-60°-140°=160°，
其每个外角为180°-160°=20°，
其边数为
| 360 |
| 20 |
故答案为：十八．
点评：本题考查了平面镶嵌，欲解答此题，要熟悉平面镶嵌的定义还要熟悉正多边形内角和外角的求法．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，⊙O的直径AB=10cm，弦CD⊥AB于E，CD=6cm．求AE的长．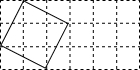
如图，一个矩形由3×6的正方形网格组成，上有4条横线和7条竖线，称为网格的网线；这些网线之间有28个交叉点，称为网格的节点，以节点为顶点，边在网线上的正方形称为网线正方形；以节点为顶点，边不在网线上的正方形称为非网线正方形，图中已经画出了一个非网线正方形．那么，在图上能够画出的非网线正方形共有某一次函数的图象经过点（-1，2），且函数y的值随自变量x的增大而减小，则下列函数符合条件的是（ ）
| A、y=4x+6 |
| B、y=-x |
| C、y=-x+1 |
| D、y=-3x+5 |