题目内容
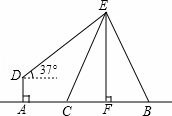
.如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
考点: 解直角三角形的应用-仰角俯角问题.
分析: 由题意可先过点D作DM⊥EF,垂足为M,在Rt△EMD中,可求出EM,进而EF=EM+MF,再在Rt△CEF中,求出CE的长.
解答: 解:过点D作DM⊥EF,垂足为M,
由题意可知四边形ADMF为矩形,
∴DM=AF=6,MF=DA=1.5,
在Rt△EMD中,EM=DM•tan∠EDM=6tan37°,
∴EF=EM+MF,DM=AF=6tan37°,
∴EF=EM+MF=6tan37°+1.5.
∵AC=3,
∴CF=AF﹣AC=3,
在Rt△CEF中,CE= ≈6.7.
≈6.7.
答:拉线CE的长为6.7米.

点评: 此题主要考查解直角三角形的应用.要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
下列图形中,不是轴对称图形的是( )
| A. | B. | C. | D. |
 闲.宾馆需对游客居住的每个房间每天支出40元的各种费用.根据规定,要提高房价,但每个房间每天的房价不得高于280元.设每个房间的房价调整为每天x元(x为10的正
闲.宾馆需对游客居住的每个房间每天支出40元的各种费用.根据规定,要提高房价,但每个房间每天的房价不得高于280元.设每个房间的房价调整为每天x元(x为10的正 整数倍).
整数倍).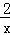 (x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .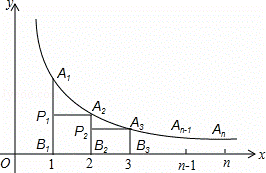
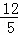 C.
C. 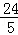 D. 5
D. 5
 记为
记为 记为 ( )
记为 ( ) B.
B. C.
C. D.
D.
 等于
等于 B.
B. D.
D.




 ,则第7个数是
,则第7个数是