题目内容
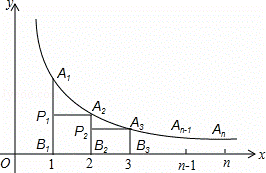
如图,在反比例函数y=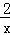 (x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(x>0)的图象上有点A1,A2,A3,…,An﹣1,An,这些点的横坐标分别是1,2,3,…,n﹣1,n时,点A2的坐标是 ;过点A1作x轴的垂线,垂足为B1,再过点A2作A2P1⊥A1B1于点P1,以点P1、A1、A2为顶点的△P1A1A2的面积记为S1,按照以上方法继续作图,可以得到△P2A2A3,…,△Pn﹣1An﹣1An,其面积分别记为S2,…,Sn﹣1,则S1+S2+…+Sn= .
(2,1) 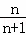
考点: 反比例函数系数k的几何意义;反比例函数图象上点的坐标特征.
专题: 规律型.
分析: 求出x=2所对应的函数值即可确定A2的坐标;根据反比例函数图象上点的坐标特征和三角形面积公式得到S1=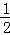 ×1×(2﹣1),S2=
×1×(2﹣1),S2=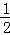 ×1×(1﹣
×1×(1﹣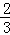 ),S3=
),S3=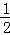 ×1×(
×1×(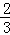 ﹣
﹣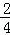 ),…,Sn=
),…,Sn= ×1×(
×1×(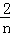 ﹣
﹣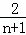 ),然后把它们相加后合并即可.
),然后把它们相加后合并即可.
解答: 解:把x=2代入y= 得y=1,
得y=1,
∴点A2的坐标为(2,1);
∵S1= ×1×(2﹣1),S2=
×1×(2﹣1),S2= ×1×(1﹣
×1×(1﹣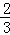 ),S3=
),S3= ×1×(
×1×(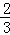 ﹣
﹣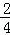 ),…,Sn=
),…,Sn= ×1×(
×1×(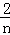 ﹣
﹣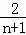 ),
),
∴S1+S2+…+Sn= (2﹣1+1﹣
(2﹣1+1﹣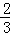 +
+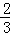 ﹣
﹣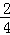 +…+
+…+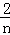 ﹣
﹣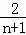 )=
)= (2﹣
(2﹣ )=
)=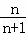 .
.
故答案为(2,1); 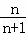 .
.
点评: 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y= 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目



 B.
B.  C.
C.  D.
D. 
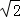 ,求正方形ADCE周长.
,求正方形ADCE周长.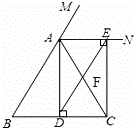
 =3 D. ﹣(﹣2)0=1
=3 D. ﹣(﹣2)0=1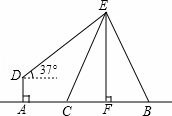
 如图,在△
如图,在△ 中,
中, ,
, 是∠
是∠ ,∠
,∠ ,则 ∠
,则 ∠ .
.