题目内容
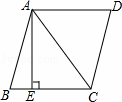
如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
A. 4 B. 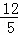 C.
C. 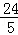 D. 5
D. 5
C考点: 菱形的性质.
专题: 几何图形问题.
分析: 连接BD,根据菱形的性质可得AC⊥BD,AO=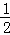 AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=
AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=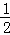 AC•BD可得答案.
AC•BD可得答案.
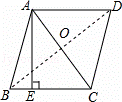
解答: 解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO=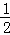 AC,BD=2BO,
AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0= =4,
=4,
∴DB=8,
∴菱形ABCD的面积是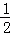 ×AC•DB=
×AC•DB=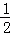 ×6×8=24,
×6×8=24,
∴BC•AE=24,
AE=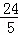 ,
,
故选:C.
点评: 此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
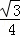 AG2.其中正确的结论( )
AG2.其中正确的结论( )

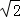 ,求正方形ADCE周长.
,求正方形ADCE周长.
 =3 D. ﹣(﹣2)0=1
=3 D. ﹣(﹣2)0=1
 的解集为 .
的解集为 .