题目内容
 如图,△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥AB于E,AE=3,AC=9.求tan∠DBC的值.
如图,△ABC中,∠C=90°,BD平分∠ABC交AC于D,DE⊥AB于E,AE=3,AC=9.求tan∠DBC的值.考点:角平分线的性质,勾股定理,锐角三角函数的定义
专题:计算题
分析:先根据角平分线的性质得DE=DC,再证明Rt△BDE≌Rt△BDC得到BC=BE,设CD=x,则DE=x,DA=AC-CD=9-x,在Rt△ADE中,根据勾股定理得到32+x2=(9-x)2,解得x=4,在Rt△ABC中得到92+BC2=(BC+3)2,解得BC=12,然后在Rt△BCD中,利用正切的定义求解.
解答:解:∵BD平分∠ABC,
而DE⊥AB,DC⊥BC,
∴DE=DC,
在Rt△BDE和Rt△BDC中,
,
∴Rt△BDE≌Rt△BDC,
∴BC=BE,
设CD=x,则DE=x,DA=AC-CD=9-x,
在Rt△ADE中,∵AE2+DE2=AD2,
∴32+x2=(9-x)2,解得x=4,
在Rt△ABC中,∵AC2+BC2=AB2,
∴92+BC2=(BC+3)2,
∴BC=12,
在Rt△BCD中,tan∠DBC=
=
=
.
而DE⊥AB,DC⊥BC,
∴DE=DC,
在Rt△BDE和Rt△BDC中,
|
∴Rt△BDE≌Rt△BDC,
∴BC=BE,
设CD=x,则DE=x,DA=AC-CD=9-x,
在Rt△ADE中,∵AE2+DE2=AD2,
∴32+x2=(9-x)2,解得x=4,
在Rt△ABC中,∵AC2+BC2=AB2,
∴92+BC2=(BC+3)2,
∴BC=12,
在Rt△BCD中,tan∠DBC=
| CD |
| BC |
| 3 |
| 12 |
| 1 |
| 4 |
点评:本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了勾股定理和锐角三角函数的定义.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
在Rt△ABC中,∠C=90°,AB=3,AC=2,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y=-3-(2+x)2的顶点坐标为( )
| A、(2,3) |
| B、(-2,3) |
| C、(-2,-3) |
| D、(2,-3) |
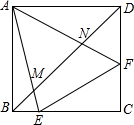 如图:正方形ABCD,∠EAF=45°.求证:
如图:正方形ABCD,∠EAF=45°.求证: 在平行四边形中,AB⊥BD,对角线AC、BD交于点O,AB=5,BD=12
在平行四边形中,AB⊥BD,对角线AC、BD交于点O,AB=5,BD=12 如图是一个物体的三视图,请画出实物原形的示意图.
如图是一个物体的三视图,请画出实物原形的示意图.