题目内容
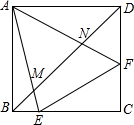如图：正方形ABCD，∠EAF=45°．求证：（1）BE+DF=EF．
（2）EF=
| 2 |
考点：旋转的性质,全等三角形的判定与性质,正方形的性质
专题：证明题
分析：（1）将△ADF绕点A顺时针旋转90°得到△ABH，根据旋转的性质可得AH=AF，BH=DF，∠DAF=∠BAH，然后求出∠EAH=∠EAF=45°，再利用“边角边”证明△AEF和△AEH全等，根据全等三角形对应边相等可得EH=EF，然后等量代换即可得证；
（2）连接AC，求出∠EAC=∠NAD，再根据正方形的对角线平分一组对角线可得∠ACE=∠ADN=45°，然后求出△ADN和△ACE相似，利用相似三角形对应边成比例可得
=
=
，同理可得△ABM和△ACF相似，然后求出
=
=
，从而得到
=
，再求出△AMN和△AFE相似，利用相似三角形对应边成比例可得
=
=
，整理即可得证．
（2）连接AC，求出∠EAC=∠NAD，再根据正方形的对角线平分一组对角线可得∠ACE=∠ADN=45°，然后求出△ADN和△ACE相似，利用相似三角形对应边成比例可得
| AN |
| AE |
| AD |
| AC |
| ||
| 2 |
| AM |
| AF |
| AB |
| AC |
| ||
| 2 |
| AN |
| AE |
| AM |
| AF |
| MN |
| EF |
| AN |
| AE |
| ||
| 2 |
解答：证明：（1）如图，将△ADF绕点A顺时针旋转90°得到△ABH，
由旋转的性质得，AH=AF，BH=DF，∠DAF=∠BAH，
∵∠EAF=45°，
∴∠EAH=∠EAF=45°，
在△AEF和△AEH中，
，
∴△AEF≌△AEH（SAS），
∴EH=EF，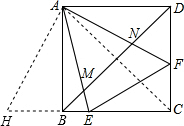
∵BE+BH=EH，
∴BE+DF=EF；
（2）连接AC，∵∠EAF=45°，
∴∠EAC+∠CAF=∠DAF+∠NAD，
∴∠EAC=∠NAD，
又∵∠ACE=∠ADN=45°，
∴△ADN∽△ACE，
∴
=
=
，
同理可得△ABM∽△ACF，
∴
=
=
，
∴
=
，
又∵∠MAN=∠FAE，
∴△AMN∽△AFE，
∴
=
=
，
∴EF=
MN．
由旋转的性质得，AH=AF，BH=DF，∠DAF=∠BAH，
∵∠EAF=45°，
∴∠EAH=∠EAF=45°，
在△AEF和△AEH中，
|
∴△AEF≌△AEH（SAS），
∴EH=EF，
∵BE+BH=EH，
∴BE+DF=EF；
（2）连接AC，∵∠EAF=45°，
∴∠EAC+∠CAF=∠DAF+∠NAD，
∴∠EAC=∠NAD，
又∵∠ACE=∠ADN=45°，
∴△ADN∽△ACE，
∴
| AN |
| AE |
| AD |
| AC |
| ||
| 2 |
同理可得△ABM∽△ACF，
∴
| AM |
| AF |
| AB |
| AC |
| ||
| 2 |
∴
| AN |
| AE |
| AM |
| AF |
又∵∠MAN=∠FAE，
∴△AMN∽△AFE，
∴
| MN |
| EF |
| AN |
| AE |
| ||
| 2 |
∴EF=
| 2 |
点评：本题考查了旋转的性质，正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，（1）利用旋转变换作出与EF长度相等EH是解题的关键，（2）难点在于求出相似三角形．
练习册系列答案
相关题目
如图，直线y=kx+1经过点A（-2，0）交y轴于点B，以线段AB为一边，向上作等腰Rt△ABC，将△ABC向右平移，当点C落在直线y=kx+1上的点F处时，平移的距离是在二次根式4
、
、
、
中，最简二次根式有（ ）
| 5 |
| 2a2 |
| b |
| 8a |
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，△ABC中，∠C=90°，BD平分∠ABC交AC于D，DE⊥AB于E，AE=3，AC=9．求tan∠DBC的值．