Question

13．如图，⊙O的半径为4，B是⊙O外一点，连接OB，且OB=6，过点B作⊙O的切线BD，切点为D，延长BO交⊙O于点A，过点A作切线BD的垂线，垂足为C．
（1）求证：AD平分∠BAC；
（2）求CD的长．

Answer 1

分析 （1）首先连接OD，由点B作⊙O的切线BD，过点A作切线BD的垂线，易证得OD∥AC，继而证得∠1=∠2=∠3，则可证得结论；
（2）易证得△BOD∽△BAC，然后由相似三角形的对应边成比例，证得结论．

解答 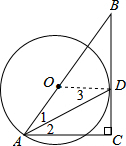（1）证明：连接OD，
∵BD是⊙O的切线，
∴OD⊥BD，
∵AC⊥BD，
∴OD∥AC，
∴∠2=∠3，
∵OA=OD，
∴∠1=∠3，
∴∠1=∠2，
即AD平分∠BAC；

（2）解：BD=$\sqrt{O{B}^{2}-O{D}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$，
∵OD∥AC，
∴△BOD∽△BAC，
∴$\frac{BD}{BC}=\frac{OB}{AB}$，
∴$\frac{2\sqrt{5}}{BC}=\frac{6}{10}$，
解得：BC=$\frac{10\sqrt{5}}{3}$．
∴CD=$\frac{4\sqrt{5}}{3}$．

点评 此题考查了切线的性质、平行线的性质以及相似三角形的判定与性质．注意准确作出辅助线是解此题的关键．