Question

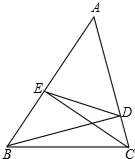在△ABC中，∠A=60°，CE、BD分别为△ABC的高，若S_△AED=2cm²，求S_△ABC．

Answer 1

考点：相似三角形的判定与性质

专题：

分析：可先证明△ADB∽△AEC，进一步可证得△AED∽△ACB，且相似比为

AE

AD

=

1

2

，再利用相似三角形的性质可求得△ABC的面积．

解答：解：∵CE、BD是△ABC的高，
∴∠ADB=∠AEC=90°，且∠EAC=∠BAD，
∴△ADB∽△AEC，
∴

AD

AE

=

AB

AC

，即

AD

AB

=

AE

AC

，且∠EAD=∠CAB，
∴△AED∽△ACB，
∵∠A=60°，
∴

AE

AC

=cos60°=

1

2

，
∴

S△ADE

S△ABC

=（

AE

AC

）²=（

1

2

）²=

1

4

，
∴

2

S△ABC

=

1

4

，
∴S_△ABC=8．

点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．注意特殊角的三角函数值．