题目内容
11.如果抛物线y=ax2+2和直线y=x+b都经过点P(2,6),那么它们图象的另一交点坐标是(-1,3).分析 由于两个函数的图象都经过点P,可将点P的坐标分别代入两个函数的解析式中,即可求出a、b的值,进一步把两个函数联立方程组求得解得出另一交点坐标.
解答 解:把点P(2,6)代入抛物线y=ax2+2,解得a=1,
把点P(2,6)代入直线y=x+b,解得b=4,
由题意得$\left\{\begin{array}{l}{y={x}^{2}+2}\\{y=x+4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$
所以它们图象的另一交点坐标是(-1,3).
故答案为:(-1,3).
点评 此题考查待定系数法求函数解析式,一次函数与二次函数的交点问题,利用联立方程组求交点坐标解决问题.

练习册系列答案
相关题目
16.若一个数的立方根是-3,则该数为( )
| A. | $-\root{3}{3}$ | B. | -27 | C. | ±$\root{3}{3}$ | D. | ±27 |
1. 图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.
图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.
 图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.
图中两条直线l1和l2的交点坐标可以看作下列方程组中( )的解.| A. | $\left\{\begin{array}{l}y=2x+1\\ y=x+2\end{array}\right.$ | B. | $\left\{\begin{array}{l}y=3x+1\\ y=x-5\end{array}\right.$ | C. | $\left\{\begin{array}{l}y=-2x+1\\ y=x-1\end{array}\right.$ | D. | $\left\{\begin{array}{l}y=-x+3\\ y=3x-5\end{array}\right.$ |
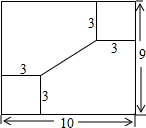 如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm.
如图,工人师傅准备在一个长、宽分别是10cm,9cm的长方形铁板上打两个小孔,小孔的圆心距两边的距离都是3cm,则两孔圆心间的距离是5cm. 如图,一个四边形木框,四边长分别为AB=8,BC=6,CD=4,AD=5,它的形状是不稳定的,求AC和BD的取值范围.
如图,一个四边形木框,四边长分别为AB=8,BC=6,CD=4,AD=5,它的形状是不稳定的,求AC和BD的取值范围. 如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.
如图,小华用一把含30°角的三角尺ABC绕直角顶点C顺时针旋转,使点A的对应点A′在边AB上.已知BC=6cm.