题目内容
4.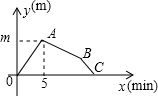 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.(1)图中点A的坐标m=500;
(2)试求家与学校之间的距离;
(3)已知弟弟从家出发时离上课还有12min,当他行至快到学校时,发现可能要迟到,于是他加快了步伐,以100m/min的速度前进,结果恰好准时到校,试求线段BC所表示的函数解析式.
分析 (1)利用图象得出可得x=5时,两人之间距离最大,进而得出m的值;
(2)由图象可得:5分钟时两人之间距离最大,此后两人之间距离不断减小,可得哥哥5分钟到达学校,进而求出家与学校之间的距离;
(3)根据题意得出弟弟加速前后行走的距离,进而得出B点坐标,再利用待定系数法求出一次函数解析式.
解答 解:(1)∵弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米,
∴如图所示,可得x=5时,两人之间距离最大,
故点A的坐标m为:5×(160-60)=500,
故答案为:500;
(2)由图象可得:5分钟时两人之间距离最大,此后两人之间距离不断减小,
可得哥哥5分钟到达学校,则家与学校之间的距离为:5×160=800(m);
答:家与学校之间的距离为800m;
(3)设弟弟以每分钟走60米的速度走了x分钟,则以100m/min的速度前进了(12-x)分钟,
故60x+100(12-x)=800,
解得:x=10,
故B点横坐标为:10,
则C点坐标为:(12,0),
B点的纵坐标为:800-10×60=200(m),
则B点坐标为:(10,200),
设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{10k+b=200}\\{12k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-100}\\{b=1200}\end{array}\right.$,
故线段BC所表示的函数解.式为:y=-100x+1200.
点评 此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识,正确得出B点坐标是解题关键.

练习册系列答案
相关题目
1.表是校女子排球队队员的年龄分布.
求校女子排球队队员的平均年龄(结果取整数,可以使用计算器)
| 年龄 | 13 | 14 | 15 | 16 |
| 频数 | 1 | 4 | 5 | 2 |
16.在△ABC中,∠C=90°,AC=$2\sqrt{5}$,∠A的角平分线交BC于D,且AD=$\frac{4}{3}\sqrt{15}$,则tanB的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{8\sqrt{3}}{3}$ |
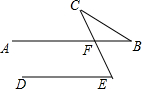 如图,AB∥DE,∠E=60°,则∠B+∠C=60°.
如图,AB∥DE,∠E=60°,则∠B+∠C=60°.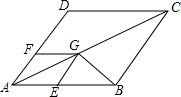 如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2.
如图,四边形ABCD和AEGF都是菱形,∠A=60°,AD=3,点E,F分别在AB,AD边上(不与端点重合),当△GBC为等腰三角形时,AF的长为3-$\sqrt{3}$或2.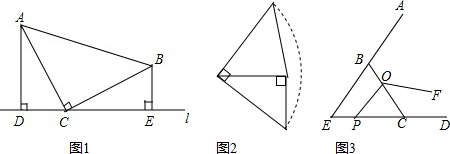
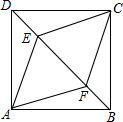 正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.
正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.