题目内容
7.如图1,梯形ABCD中,AD∥BC,∠D=90°,∠ABC=60°,CD=3$\sqrt{3}$,AD=16,点P是AD边上的一动点.(1)若tan∠PCB=$\frac{{3\sqrt{3}}}{4}$,求AP的长;
(2)如图2,若∠CPB=120°,
①△PCB与△ABP相似吗?为什么?
②求AP的长.
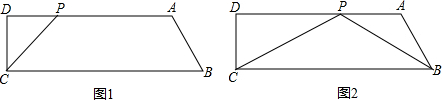
分析 (1)根据AD∥BC,得到∠DPC=∠PCB,根据正切的概念求出DP的长,根据AP=AD-PD求出AP的长;
(2)①根据AD∥BC,得到∠APB=∠PBC,又∠A=∠CPB=120°,根据两组对应角相等的两个三角形相似得到答案;
②过B作BE⊥DA于E,根据直角三角形的性质求出AE的长,得到BC的长,设PA=x,由△PCB∽△ABP,用x表示出PB2,根据勾股定理列出方程,解方程得到答案.
解答 解:(1)∵AD∥BC,∴∠DPC=∠PCB,
∴tan∠DPC=$\frac{CD}{DP}$=$\frac{{3\sqrt{3}}}{4}$,又CD=3$\sqrt{3}$,
∴DP=4,
∴AP=AD-PD=12;
(2)①相似.
理由:∵AD∥BC,∠ABC=60°,
∴∠APB=∠PBC,∠A=120°,
∴∠A=∠CPB=120°,
∴△PCB∽△ABP;
②如图2,过B作BE⊥DA于E,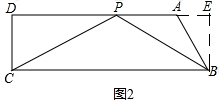
∵∠ABE=30°,BE=CD=3$\sqrt{3}$,
∴AE=3,则BC=19,
设PA=x,
由△PCB∽△ABP,得PB2=PA•BC=19x,
则在△PBE中由勾股定理得:${(x+3)^2}+{(3\sqrt{3})^2}=19x$,
解得:x1=4,x2=9,
则AP的长为4或9.
点评 本题考查的是相似三角形的判定和性质,正确作出辅助线、灵活运用锐角三角函数的概念和相似三角形的判定定理、性质定理是解题的关键.

练习册系列答案
相关题目
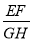 的值是( )
的值是( )
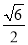 B.
B. 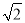 C.
C. 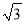 D. 2
D. 2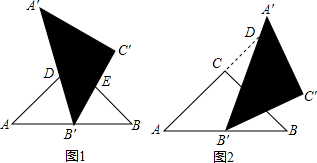
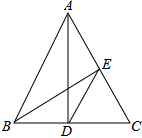 已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.
已知,如图,在△ABC中,∠C=60°,AD⊥BC于D,BE⊥AC于E,下列结论:①$\frac{AC}{BC}$=$\frac{AD}{BE}$,②$\frac{AE}{BD}$=$\frac{AD}{BE}$,③$\frac{CD}{CE}$=$\frac{AC}{BC}$,④AB=2DE.其中正确的有(填序号)①③④.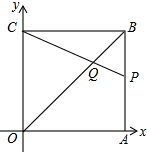 如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
如图,在平面直角坐标系中,四边形OABC是边长为2的正方形,顶点A,C分别在x,y轴的正半轴上,点Q在对角线OB上,且QO=OC,连接CQ并延长CQ交边AB于点P,则点P与Q的坐标分别为(2,4-2$\sqrt{2}$)、($\sqrt{2},\sqrt{2}$).
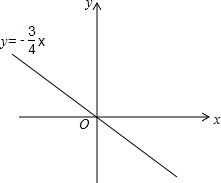 在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.
在平面直角坐标系xOy中,将直线y=-$\frac{3}{4}$x沿y轴向上平移6个单位后,分别与x轴、y轴相交于A,B两点.