题目内容

10．先化简，再求值：（x-$\frac{{x}^{2}+2}{x+2}$）÷$\frac{x-1}{{x}^{2}+2x}$-$\frac{2x}{x+1}$，其中x满足x2-x-1=0．

分析 原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分后两项通分并利用同分母分式的减法法则计算，得到最简结果，把已知等式变形后代入计算即可求出值．

解答 解：原式=$\frac{x（x+2）-{x}^{2}-2}{x+2}$•$\frac{x（x+2）}{x-1}$-$\frac{2x}{x+1}$=$\frac{2（x-1）}{x+2}$•$\frac{x（x+2）}{x-1}$-$\frac{2x}{x+1}$=2x-$\frac{2x}{x+1}$=$\frac{2x（x+1）-2x}{x+1}$=$\frac{2{x}^{2}}{x+1}$，
由x2-x-1=0，得到x2=x+1，
则原式=2．

点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案
相关题目
17．如图，∠1和∠2是对顶角的图形是（　　）
A．B．C．D．
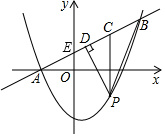18．如图，在平面直角坐标系中，直线y=$\frac{1}{2}$x+1与y轴交于点E，与抛物线y=ax2+bx-3交于A，B两点，点A在x轴上，点B的纵坐标为3，点P是直线AB下方的抛物线上一动点（不用A，B重合），且点P的横坐标为m，过点P作x轴的垂线交直线AB与点C，作PD⊥AB于点D．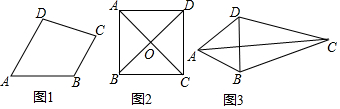
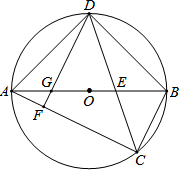（1）求抛物线的解析式；
（2）①求sin∠ACP的值；
         ②求线段PD的最大值；
（3）连接PB，线段PC把△PBD分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为9：10？若存在，求出m值；若不存在，请说明理由．
15．等腰三角形是生活中常见的几何图形，我们称有两边相等的三角形是等腰三角形，类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”．
（1）如图1，在四边形ABCD中添加一个条件AB=BC，使得四边形ABCD是“等邻边四边形”；
（2）如图2，“等邻边四边形”ABCD中，AB=AD，AC=BD，且对角线AC、BD互相平分，请你证明“等邻边四边形”ABCD是正方形；
（3）如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD=90°，AC、BD为对角线，AC=$\sqrt{5}$AB，试探究BC、CD、BD之间的数量关系，并证明你的结论．
5．要使$\sqrt{\frac{8}{x-2}}$有意义，则x的取值范围是（　　）
A．x＜2B．x＞2C．x≤2D．x＞0且x≠2
15．先化简，再求值：
（1）已知分式$\frac{{a}^{2}+4{b}^{2}+4ab}{{a}^{2}-4{b}^{2}}$，其中a=3，b=$\frac{1}{2}$；
（2）已知$\frac{a-b}{ab}=-2$，求$\frac{2a+ab-2b}{a-ab-b}$的值．
2．已知关于x的一元二次方程（x-m）2+3x=2m-3有两个实数根．
（1）求m的取值范围；
（2）设方程的两实根分别为x1与x2，求代数式x1•x2-x12-x22的最大值．
19．如图，AB为⊙O的直径，弦CD平分∠ACB，CD交OB于点E．DF⊥AC于点F，交AO于点G．
（1）求证：△EDG∽△EAD；
（2）若EG=10，EA=16，求⊙O的半径
（3）求证：DF=BC+AF．
20．已知菱形的边长是6，一个内角是60°，则这个菱形较长的对角线长为6$\sqrt{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网