题目内容
11.对于每个非零自然数n,抛物线y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$与x轴交于An、Bn两点,以AnBn表示这两点间的距离,则A1B1+A2B2+…+A2017B2017的值是( )| A. | $\frac{2015}{2016}$ | B. | $\frac{2016}{2017}$ | C. | $\frac{2017}{2018}$ | D. | 1 |
分析 首先求出抛物线与x轴两个交点坐标,然后由题意得到AnBn=$\frac{1}{n}$-$\frac{1}{n+1}$,进而求出A1B1+A2B2+…+A2017B2017的值.
解答 解:令y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=0,
即x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$=0,
解得x=$\frac{1}{n}$或x=$\frac{1}{n+1}$,
故抛物线y=x2-$\frac{2n+1}{n(n+1)}$x+$\frac{1}{n(n+1)}$与x轴的交点为($\frac{1}{n}$,0),($\frac{1}{n+1}$,0),
由题意得AnBn=$\frac{1}{n}$-$\frac{1}{n+1}$,
则A1B1+A2B2+…+A2017B2017=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2017}$-$\frac{1}{2018}$=1-$\frac{1}{2018}$=$\frac{2017}{2018}$,
故选C.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是用n表示出抛物线与x轴的两个交点坐标,此题难度不大.

练习册系列答案
相关题目
16.计算$\sqrt{4}$的结果是( )
| A. | -2 | B. | ±2 | C. | 2 | D. | 4 |
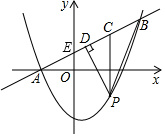 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+1与y轴交于点E,与抛物线y=ax2+bx-3交于A,B两点,点A在x轴上,点B的纵坐标为3,点P是直线AB下方的抛物线上一动点(不用A,B重合),且点P的横坐标为m,过点P作x轴的垂线交直线AB与点C,作PD⊥AB于点D.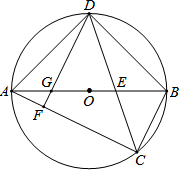 如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G.
如图,AB为⊙O的直径,弦CD平分∠ACB,CD交OB于点E.DF⊥AC于点F,交AO于点G. 如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).
如图,在平行四边形ABCD中,添加一个条件使它成为一个矩形,你添的条件是AC=BD(不唯一).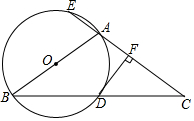 如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.
如图,△ABC中,AB=AC,以AB为直径的O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.