题目内容
3.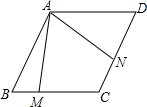 如图,在?ABCD中,∠ABC=60°,AB=BC=6cm,点M、N分别在BC和CD上,且∠MAN=60°,则四边形AMCN的面积是多少( )
如图,在?ABCD中,∠ABC=60°,AB=BC=6cm,点M、N分别在BC和CD上,且∠MAN=60°,则四边形AMCN的面积是多少( )| A. | 6cm2 | B. | 18cm2 | C. | 9$\sqrt{3}$cm2 | D. | 8$\sqrt{3}$cm2 |
分析 连接AC,通过证明△ABM和△ANC全等可知四边形AMCN的面积正好等于平行四边形面积的一半.
解答 解:连接AC,
∵∠B=60°,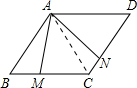
∴∠BAD=120°,
∵∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABC为等边三角形,
∴AB=AC,
∴△ABM≌△ACN,
∴四边形AMCN的面积等于平行四边形面积的一半.
∵AB=6cm,
∴BC边上的高为3$\sqrt{3}$,S菱形ABCD=6×$3\sqrt{3}$=18$\sqrt{3}$,
∴四边形AMCN的面积等于$\frac{1}{2}$×18$\sqrt{3}$=9$\sqrt{3}$.
故选C.
点评 本题考查了等边三角形的判定和性质、平行四边形的性质、平行四边形的面积公式以及勾股定理的运用,题目比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.不等式2x<4的解集为( )
| A. | x<$\frac{1}{2}$ | B. | x<2 | C. | x>$\frac{1}{2}$ | D. | x>2 |
14.已知点A(-1,y1),A(-3,y2)都在反比例函数y=$\frac{k}{x}$(k>0)的图象上,则y1与y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
11.下列给出的条件中不能判定一个四边形是矩形的是( )
| A. | 一组对边平行且相等,一个角是直角 | |
| B. | 对角线互相平分且相等 | |
| C. | 有三个角是直角 | |
| D. | 一组对边平行,另一组对边相等,且对角线相等 |
18. 如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
 如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )
如图,在?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于点E,则BE的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
8. 如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )
如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )
 如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )
如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )| A. | y=2x-5 | B. | y=2x2+7 | C. | y=$\frac{1}{x(x+1)}$ | D. | y=$\sqrt{x+2}$ |
12. 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (1,3) | B. | (3,2) | C. | (0,3) | D. | (-3,3) |