题目内容
18．
如图，在?ABCD中，AD=8，AB=6，DE平分∠ADC交BC于点E，则BE的长是（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 由四边形ABCD是平行四边形，可得BC=AD=8，CD=AB=6，AD∥BC，得∠ADE=∠DEC，又由DE平分∠ADC，可得∠CDE=∠DEC，根据等角对等边，可得EC=CD=6，所以求得BE=BC-EC=2．
解答 解：∵四边形ABCD是平行四边形，
∴BC=AD=8，CD=AB=6，AD∥BC，
∴∠ADE=∠DEC，
∵DE平分∠ADC，
∴∠ADE=∠CDE，
∴∠CDE=∠DEC，
∴EC=CD=6，
∴BE=BC-EC=2．
故选A．
点评 此题考查了平行四边形的性质、角平分线的定义与等腰三角形的判定定理．注意当有平行线和角平分线出现时，会出现等腰三角形．
练习册系列答案
相关题目
如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO．有下列结论：
9．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
6．在平面直角坐标系中，点P在x轴上方，且点P到x轴的距离为2，到y轴的距离为3，则点P的坐标为（ ）
| A． | （2，3） | B． | （3，2） | C． | （-3，2）或（3，2） | D． | （-2，3）或（2，3） |
3．
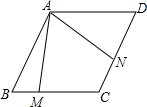如图，在?ABCD中，∠ABC=60°，AB=BC=6cm，点M、N分别在BC和CD上，且∠MAN=60°，则四边形AMCN的面积是多少（ ）
如图，在?ABCD中，∠ABC=60°，AB=BC=6cm，点M、N分别在BC和CD上，且∠MAN=60°，则四边形AMCN的面积是多少（ ）| A． | 6cm2 | B． | 18cm2 | C． | 9$\sqrt{3}$cm2 | D． | 8$\sqrt{3}$cm2 |
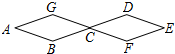如图，两个完全相同的菱形其边长为1厘米，一只蚂蚁由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动，行走2017厘米后停下，则这只蚂蚁停在B点．
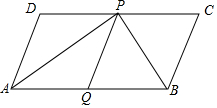如图，在?ABCD中，AP是BP分别平分∠DAB和∠CBA，PQ∥AD，若AD=5cm，AP=8cm，则△ABP的面积等于（ ）cm2．