题目内容
16. 如图,△ABC中,BF、CF分别是∠ABC和∠ACB的平分线,DF∥BC交AC于E,若△ABC的周长为15,BC=4,则△ADE的周长为( )
如图,△ABC中,BF、CF分别是∠ABC和∠ACB的平分线,DF∥BC交AC于E,若△ABC的周长为15,BC=4,则△ADE的周长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 根据角平分线的定义可得∠FBD=∠FBC,∠ECF=∠FCB,再根据两直线平行,内错角相等可得∠FBC=∠BFD,∠FCB=∠CFE,然后求出∠FBD=∠DFB,∠FCF=∠CFE,再根据等角对等边可得ED=BD,EF=CE,即可得出DE=BD+CE;求出△ADE的周长=AB+AC,然后代入数据进行计算即可得解.
解答 解:∵F是∠ABC,∠ACB平分线的交点,
∴∠FBD=∠FBC,∠ECF=∠FCB,
∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∴∠DFB=∠DBF,∠EFC=∠FCE,
∴DF=BD,EF=CE,
∴DE=DF+EF=BD+CE,
即DE=BD+CE,
∴△ADE的周长=AD+DE+AE=(AD+BD)+(CE+AE)=AB+AC,
∵△ABC的周长为15,BC=4,
∴AB+AC=11,
∴△ADE的周长=11,
故选D.
点评 本题考查了等腰三角形的判定与性质,平行线的性质,主要利用了角平分线的定义,等角对等边的性质,两直线平行,内错角相等的性质,熟记各性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.下列命题中正确的是( )
| A. | 有一组邻边相等的四边形是菱形 | |
| B. | 对角线相等的平行四边形是矩形 | |
| C. | 对角线垂直的平行四边形是正方形 | |
| D. | 一组对边平行的四边形是平行四边形 |
11.下列运算正确的是( )
| A. | x•x7=x8 | B. | x8÷x4=x2 | C. | (xy2)3=xy6 | D. | (x3)2=x5 |
1.方程组$\left\{\begin{array}{l}{x-y=1}\\{2x+y=5}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ |
8.下列说法正确的是( )
| A. | 一个角的补角一定大于这个角 | |
| B. | 任何一个角都有余角 | |
| C. | 若∠1+∠2+∠3=90°,则∠1,2,∠3互余 | |
| D. | 若一个角有余角,则这个角的补角与这个角的余角的差为90° |
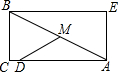 如图,矩形ACBE中,AC=12,BC=5,点M在边AB上,且AM=6,动点D在矩形边上运动一周,能使△ADM是以∠AMD为顶角的等腰三角形共有( )
如图,矩形ACBE中,AC=12,BC=5,点M在边AB上,且AM=6,动点D在矩形边上运动一周,能使△ADM是以∠AMD为顶角的等腰三角形共有( )