题目内容
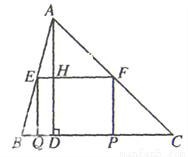
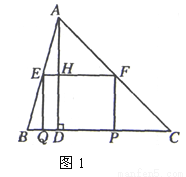
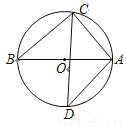
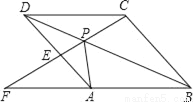
如图,在△ABC中,∠C=45°,BC=10,高AD=8,矩形EFPQ的一边QP在BC边上,E、F两点分别在AB、AC上,AD交EF于点H.
(1)求证: 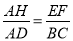 ;
;
(2)设EF=x,当x为何值时,矩形EFPQ的面积最大?并求其最大值;
(3)当矩形EFPQ的面积最大时,该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动),设运动时间为t秒,矩形EFFQ与△ABC重叠部分的面积为S,求S与t的函数关系式.
【答案】(1)证明见解析;(2)当x=5时,S矩形EFPQ有最大值,最大值为20;(3)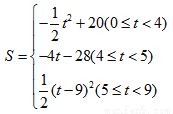
【解析】试题分析:(1)本题利用相似三角形的性质——相似三角形的对应边上的高之比等于相似比解决;(2)根据第一问的结论,即可根据矩形的面积公式得到关于矩形EFPQ的面积和x的函数关系式,根据函数的性质即可得到矩形的最大面积及对应的x的值;(3)此题要理清几个关键点,当矩形的面积最大时,由(2)可知此时EF=5,EQ=4;易证得△CPF是等腰Rt△,则PC=PF=4,QC=QP+PC=9;
一、P、C重合时,矩形移动的距离为PC(即4),运动的时间为4s;
二、E在线段AC上时,矩形移动的距离为9-4=5,运动的时间为5s;
三、Q、C重合时,矩形运动的距离为QC(即9),运动的时间为9s;
所以本题要分三种情况,分别写出解析式即可.
试题解析:
(1)∵ 四边形EFPQ是矩形,∴ EF∥QP.∴ △AEF∽△ABC.
又∵ AD⊥BC,
∴ AH⊥EF,∴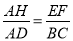
(2)由(1)得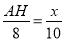 ,∴ AH=
,∴ AH=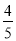 x.
x.
∴ EQ=HD=AD-AH=8-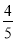 x,
x,
∴ S矩形EFPQ=EF·EQ=x (8-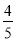 x) =-
x) =-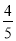 x2+8 x=-
x2+8 x=-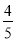 (x-5)2+20.
(x-5)2+20.
∵ -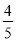 <0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20.
<0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20.
(3)如图1,由(2)
得EF=5,EQ=4.
∵∠C=45°,∴ △FPC是等腰直角三角形.
∴ PC=FP=EQ=4,QC=QP+PC=9.
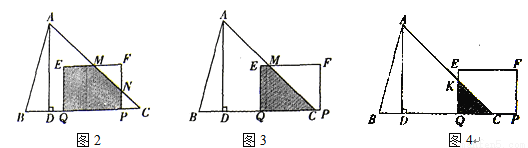
分三种情况讨论:① 如图2.当0≤t<4时,
设EF、PF分别交AC于点M、N,则△MFN是等腰直角三角形,
∴ FN=MF=t.
∴S=S矩形EFPQ-SRt△MFN=20-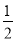 t2=-
t2=-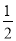 t2+20;
t2+20;
②如图3,当4≤t<5时,则ME=5-t,QC=9-t.
∴ S=S梯形EMCQ=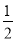 [(5-t)+(9-t )]×4=-4t+28;
[(5-t)+(9-t )]×4=-4t+28;
③如图4,当5≤t≤9时,设EQ交AC于点K,则KQ=QC=9-t.
∴ S=S△KQC=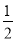 (9-t)2=
(9-t)2=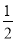 ( t-9)2.
( t-9)2.
综上所述:S与t的函数关系式为:
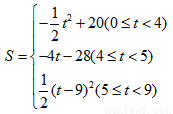
点睛:此题主要考查了矩形、等腰直角三角形的性质,相似三角形的判定和性质及二次函数的应用等知识,同时还考查了分类讨论的数学思想.
【题型】解答题
【结束】
12
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k,使得x1·x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
(1)当k≤时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立 【解析】试题分析:(1)根据一元二次方程根的判别式列出不等式,解之即可;(2)本题利用韦达定理解决. 试题解析: (1) ,解得 (2)由 , 由根与系数的关系可得: 代入得: , 化简得: , 得. 由于的取值范围为, 故不存在k使。 ... 阅读快车系列答案
阅读快车系列答案

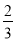 B.
B.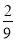 C.
C.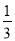 D.
D.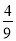
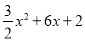 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.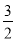 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;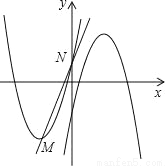
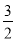 x2+6x﹣2(3)当q=
x2+6x﹣2(3)当q= 时,3﹣4q取最大值,最大值为﹣7
时,3﹣4q取最大值,最大值为﹣7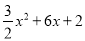 中x=0,则y=2,
中x=0,则y=2,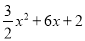 =
=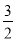 (x+2)2﹣4, ∴M(﹣2,﹣4).
(x+2)2﹣4, ∴M(﹣2,﹣4).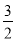 x2+6x+2<kx+b的解集为﹣2<x<0.
x2+6x+2<kx+b的解集为﹣2<x<0. 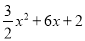 的顶点为M(﹣2,﹣4),
的顶点为M(﹣2,﹣4),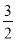 (x﹣2)2+4=﹣
(x﹣2)2+4=﹣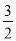 x2+6x﹣2.
x2+6x﹣2. 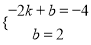 ,解得:
,解得: 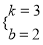 ,
,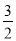 x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,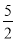 . ∵﹣4<0,
. ∵﹣4<0,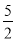 时,3﹣4q取最大值,最大值为﹣7.
时,3﹣4q取最大值,最大值为﹣7.

 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.
 ,
,  ,
,  ,
, 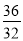 ,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.
,……中得到巴尔末公式,从而打开光谱奥妙的大门。请你根据以上光谱数据的规律写出它的第七个数据_______________.