题目内容
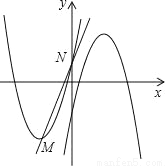
如图,在平面直角坐标系中,已知抛物线C1:y=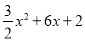 的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
的顶点为M,与y轴相交于点N,先将抛物线C1沿x轴翻折,再向右平移p个单位长度后得到抛物线C2:直线l:y=kx+b经过M,N两点.
(1)结合图象,直接写出不等式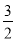 x2+6x+2<kx+b的解集;
x2+6x+2<kx+b的解集;
(2)若抛物线C2的顶点与点M关于原点对称,求p的值及抛物线C2的解析式;
(3)若直线l沿y轴向下平移q个单位长度后,与(2)中的抛物线C2存在公共点,
求3﹣4q的最大值.
【答案】(1)﹣2<x<0(2)y=﹣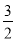 x2+6x﹣2(3)当q=
x2+6x﹣2(3)当q= 时,3﹣4q取最大值,最大值为﹣7
时,3﹣4q取最大值,最大值为﹣7
【解析】试题分析:(1)、首先根据二次函数的解析式分别求出点M和点N的坐标,然后根据图像得出不等式的取值范围;(2)、根据翻折得出抛物线的顶点坐标和开口方向以及大小,从而得出抛物线的函数解析式;(3)、首先将点M和点N的坐标代入一次函数解析式得出一次函数的解析式,然后设平移后的解析式为y=3x+2-q,然后根据与抛物线有交点得出方程有实数根,从而得出最大值.
试题解析:(1)令y=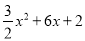 中x=0,则y=2,
中x=0,则y=2,
∴N(0,2); ∵y=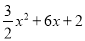 =
=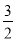 (x+2)2﹣4, ∴M(﹣2,﹣4).
(x+2)2﹣4, ∴M(﹣2,﹣4).
观察函数图象,发现:当﹣2<x<0时,抛物线C1在直线l的下方,
∴不等式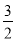 x2+6x+2<kx+b的解集为﹣2<x<0.
x2+6x+2<kx+b的解集为﹣2<x<0.
(2)∵抛物线C1:y=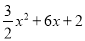 的顶点为M(﹣2,﹣4),
的顶点为M(﹣2,﹣4),
沿x轴翻折后的对称点坐标为(﹣2,4). ∵抛物线C2的顶点与点M关于原点对称,
∴抛物线C2的顶点坐标为(2,4), ∴p=2﹣(﹣2)=4.
∵抛物线C2与C1开口大小相同,开口方向相反,
∴抛物线C2的解析式为y=﹣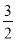 (x﹣2)2+4=﹣
(x﹣2)2+4=﹣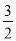 x2+6x﹣2.
x2+6x﹣2.
(3)将M(﹣2,﹣4)、N(0,2)代入y=kx+b中,得: 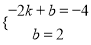 ,解得:
,解得: 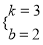 ,
,
∴直线l的解析式为y=3x+2.
∵若直线l沿y轴向下平移q个单位长度后与抛物线C2存在公共点,
∴方程﹣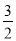 x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
x2+6x﹣2=3x+2﹣q有实数根,即3x2﹣6x+8﹣2q有实数根,
∴△=(﹣6)2﹣4×3×(8﹣2q)≥0,解得:q≥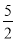 . ∵﹣4<0,
. ∵﹣4<0,
∴当q=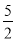 时,3﹣4q取最大值,最大值为﹣7.
时,3﹣4q取最大值,最大值为﹣7.
点睛:本题主要考查的就是二次函数的图形与性质、一次函数的性质、二次函数与一次函数的大小比较的方法以及函数与方程之间的关系,属于中上难度的题目.在解答函数大小比较的题目时,我们首先根据方程的思想得出两个函数的交点坐标,然后过交点作x轴的垂线,然后根据函数所处的位置进行比较大小得出答案;函数关于x轴对称,则顶点坐标的纵坐标变为相反数,开口方向发生改变,开口大小不改变;在求直线与抛物线是否有交点时,则联立成方程,然后根据一元二次方程根的判别式来进行判定.
【题型】解答题
【结束】
17
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
(1); (2),当时, ; (3)当销售单价为元时,在全部收回投资的基础上使第二个月的利润不低于1700元. 【解析】【试题分析】(1)根据表格的数据.易得销售单价每升高5元,销售量下降10Kg,即w是x的一次函数,故设设,将(70,100),(75,90)代入上式得: 解得: ,则; (2)销售利润=单位质量的利润乘以销售量,即 ,化为顶点式得, ,当时, ...

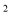 -ax+a
-ax+a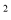 -4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.
-4a-4与x轴相交于点A和点B,与y轴相交于点D(0,8),直线DC平行于x轴,交抛物线于另一点C,动点P以每秒2个单位长度的速度从C点出发,沿C→D运动,同时,点Q以每秒1个单位长度的速度从点A出发,沿A→B运动,连接PQ、CB,设点P运动的时间为t秒.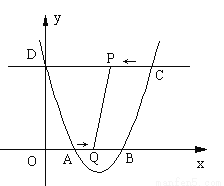
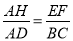 ;
;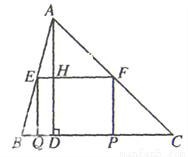
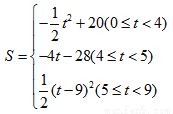
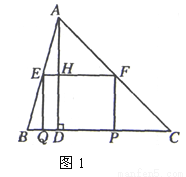
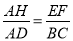
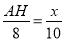 ,∴ AH=
,∴ AH=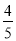 x.
x.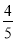 x,
x,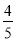 x) =-
x) =-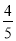 x2+8 x=-
x2+8 x=-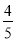 (x-5)2+20.
(x-5)2+20.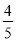 <0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20.
<0, ∴ 当x=5时,S矩形EFPQ有最大值,最大值为20. 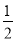 t2=-
t2=-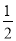 t2+20;
t2+20;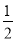 [(5-t)+(9-t )]×4=-4t+28;
[(5-t)+(9-t )]×4=-4t+28;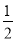 (9-t)2=
(9-t)2=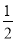 ( t-9)2.
( t-9)2. 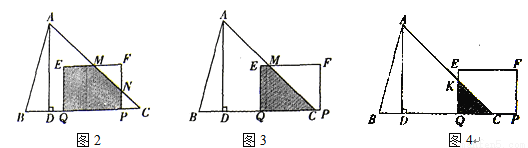
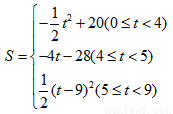
 的值.
的值.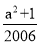 =
= .
.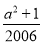 =-a-1+
=-a-1+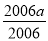 =-1,即a2-2007a+
=-1,即a2-2007a+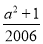 =-1.
=-1.
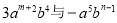 的和仍是一个单项式,则
的和仍是一个单项式,则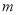 +
+ 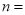 _____________________
_____________________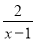 有意义,则x的取值范围是
有意义,则x的取值范围是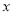 ≠1 B. x>1 C. x=1 D. x<1
≠1 B. x>1 C. x=1 D. x<1