题目内容
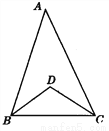
(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB的平分线相交于点D,求∠BDC的度数.
(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
题目内容
(1)如图,在△ABC中,∠A=42°,∠ABC和∠ACB的平分线相交于点D,求∠BDC的度数.
(2)在(1)中去掉∠A=42°这个条件,请探究∠BDC和∠A之间的数量关系.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案