题目内容
9.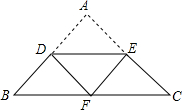 如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
如图,在△ABC中,AB=AC,DE∥BC,现将△ABC沿DE进行折叠,使点A恰好落在BC上的点F处,则△FDE与△ABC的周长比为1:2.
分析 连接AF,由翻折的性质可知AG=AF=1:2,△FDE的周长=△ADE的周长,由DE∥BC可知△ADE∽△ABC,依据相似三角形的周长之比=相似比=对应高的比求解即可.
解答 解:如图所示:连接AF.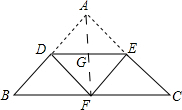
由翻折的性质可知:AG=GF,AG⊥DE,△FDE的周长=△ADE的周长.
∵ED∥BC,
∴AF⊥BC.
∴$\frac{AD}{AB}=\frac{AG}{AF}$=$\frac{1}{2}$.
∵DE∥BC,
∴△ADE∽△ABC.
∴△FDE与△ABC的周长比为=1:2.
故答案为:1:2.
点评 本题主要考查的是翻折的性质、相似三角形的性质和判定、根据翻折的性质求得AD:AB=1:2是解题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
20.下列事件中是必然事件的是( )
| A. | 平安夜下雪 | B. | 地球在自转的同时还不停的公转 | ||
| C. | 所有人15岁时身高必达到1.70米 | D. | 下雨时一定打雷 |
4.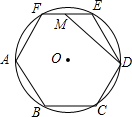 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
 如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )
如图,正六边形ABCDEF内接于⊙O,M为EF的中点,连接DM,若⊙O的半径为2,则MD的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
14.如图,在“妙手推推推”的游戏中,主持人出示了一个9位数,让参加者猜商品价格.被猜的价格是一个4位数,也就是这个9位中从左到右连在一起的某4个数字.如果参与者不知道商品的价格,从这些连在一起的所有4位数中,任意猜一个,求他猜中该商品价格的概率( )

| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
18.某市因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
| 租金(单位:元/台•时) | 挖掘土石方量(单位:m3/台•时) | |
| 甲型挖掘机 | 120 | 80 |
| 乙型挖掘机 | 100 | 60 |
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案?
19.如果x=6是方程2x+3a=6x的解,那么a的值是( )
| A. | 4 | B. | 8 | C. | 9 | D. | -8 |
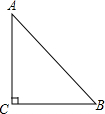 如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.