题目内容
12.先化简,再求值:($\frac{x}{x-2}$-$\frac{x}{x+2}$)÷($\frac{2x}{x+2}$),其中x=2sin60°+2tan45°.分析 先根据分式混合运算的法则把原式进行化简,再取出x的值代入进行计算即可.
解答 解:原式=$\frac{x(x+2)-x(x-2)}{(x-2)(x+2)}$•$\frac{x+2}{2x}$
=$\frac{4x}{(x-2)(x+2)}$•$\frac{x+2}{2x}$
=$\frac{2}{x-2}$,
当x=2sin60°+2tan45°=2×$\frac{\sqrt{3}}{2}$+2=2+$\sqrt{3}$时,原式=$\frac{2}{2+\sqrt{3}-2}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3.甲、乙两人沿同一个方向到同一个地点去,甲一半时间以速度a行走,另一半时间以速度b行走(b≠a);乙一半的路程以速度a行走,另一半路程以速度b行走,则先到达目的地的是( )
| A. | 甲 | B. | 乙 | C. | 同时到达 | D. | 与路程有关 |
17.在下列各组数中,三个数为勾股数的是( )
| A. | 2,3,4 | B. | 3,4,5 | C. | 4,5,6 | D. | 6,8,12 |
4.用科学记数法表示52000000正确的是( )
| A. | 52×107 | B. | 5.2×108 | C. | 5.2×107 | D. | 52×108 |
2.因春节放假,某工厂2月份产量比1月份下降了5%,3月份将恢复正常,预计3月份产量将比2月份增长15%.设2、3月份的平均增长率为x,则x满足的方程是( )
| A. | 15%-5%=x | B. | 15%-5%=2x | C. | (1-5%)(1+15%)=2(1+x) | D. | (1-5%)(1+15%)=(1+x)2 |
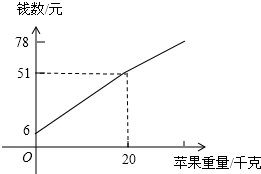 李大爷从家里的果园中摘了若干千克苹果.到城内出售,为了方便,他自带了一些零钱,将苹果按原来的市场价格出售一些后,由于急着回家,于是按原价的八折出售直到售完为止,售出苹果的千克数与他手中持有的钱数(含备用零钱)的关系如图所示,问:
李大爷从家里的果园中摘了若干千克苹果.到城内出售,为了方便,他自带了一些零钱,将苹果按原来的市场价格出售一些后,由于急着回家,于是按原价的八折出售直到售完为止,售出苹果的千克数与他手中持有的钱数(含备用零钱)的关系如图所示,问: 已知:关于x的方程mx2-(3m+1)x+2m+2=0(m>1).
已知:关于x的方程mx2-(3m+1)x+2m+2=0(m>1).