题目内容
3.甲、乙两人沿同一个方向到同一个地点去,甲一半时间以速度a行走,另一半时间以速度b行走(b≠a);乙一半的路程以速度a行走,另一半路程以速度b行走,则先到达目的地的是( )| A. | 甲 | B. | 乙 | C. | 同时到达 | D. | 与路程有关 |
分析 甲乙二人相同的距离,时间、速度不同,因此可设总路程为1.乙到达目的地所用的时间为t1,甲到达目的地所用的时间为t2,由题意可得:t1=$\frac{\frac{1}{2}}{a}$+$\frac{\frac{1}{2}}{b}$=$\frac{a+b}{2ab}$;又$\frac{{t}_{2}}{2}$a+$\frac{{t}_{2}}{2}$b=1,所以t2=$\frac{2}{a+b}$,将t1、t2做差即可求出二者时间关系,即可求得答案.
解答 解:设总路程为单位1,乙到达目的地所用的时间为t1,甲到达目的地所用的时间为t2.
由题意可得:t1=$\frac{\frac{1}{2}}{a}$+$\frac{\frac{1}{2}}{b}$=$\frac{a+b}{2ab}$,
又∵$\frac{{t}_{2}}{2}$a+$\frac{{t}_{2}}{2}$b=1,
∴t2=$\frac{2}{a+b}$,
∴t1-t2=$\frac{a+b}{2ab}$-$\frac{2}{a+b}$=$\frac{(a+b)^{2}-4ab}{2ab(a+b)}$>0,
∴t1>t2,
(因为根据题意可得a≠b)所以乙先到.
故选:A.
点评 本题考查了列代数式,找到合适的等量关系是解决问题的关键.本题是一道考查行程问题的应用题,解此类问题只要把握住路程=速度×时间,即可找出等量关系,列出方程.要注意找出题中隐含的条件,如本题甲乙二人相同的行驶路程.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
14.∠α与∠β的两边分别平行,∠α的度数是70°,则∠β的度数是( )
| A. | 70° | B. | 80° | C. | 110° | D. | 70°或110° |
11.春天是气温变化较大的季节,某地气象部门将2012年3月1日~6日和2013年3月1日~6日每天的最高气温统计如下表:
(1)分别求出2012年3月1日~6日和2013年3月1日~6日的平均气温和方差各是多少?
(2)利用(1)的结果,你来分析一下,2012年3月1日~6日和2013年3月1日~6日相比,哪个时间段的气温相对较高?哪个时间段的气温相对较稳定?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
| 2012年3月 | 3℃ | 5℃ | 3℃ | 5℃ | 6℃ | 8℃ |
| 2013年3月 | 6℃ | 6℃ | 11℃ | 14℃ | 15℃ | 14℃ |
(2)利用(1)的结果,你来分析一下,2012年3月1日~6日和2013年3月1日~6日相比,哪个时间段的气温相对较高?哪个时间段的气温相对较稳定?
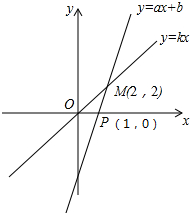 如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.
如图,一次函数y=ax+b的图象与正比例函数y=kx的图象交于点M.