题目内容
1. 已知:关于x的方程mx2-(3m+1)x+2m+2=0(m>1).
已知:关于x的方程mx2-(3m+1)x+2m+2=0(m>1).(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2),若y是关于m的函数,且y=mx2-2x1,求这个函数的解析式;
(3)将(2)中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象回答:当关于m的函数y=2m+b的图象与此图象有两个公共点时,b的取值范围是b<-5(直接写出答案).
分析 (1)要证明无论m取何值方程必有两个不相等的实数根,只要证明△≥0即可,而,△=(3m+1)2-4m(2m+2)=(m-1)2.由m>1,可得到△>0;
(2)利用求根公式可得$x=\frac{{3m+1±\sqrt{{{({m-1})}^2}}}}{2m}=\frac{{3m+1±({m-1})}}{2m}$,因为m>1,x1>x2.所以${x_1}=2,{x_2}=1+\frac{1}{m}$.然后代入y=mx2-2x1,即可得到函数的解析式即可;
(3)先求出对折后的函数的解析式,进而求得与函数y=2m+b的交点坐标,根据题意列出不等式组,解不等式组即可求得.
解答 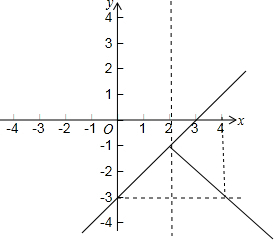 (1)证明:由题意得,△=(3m+1)2-4m(2m+2)=(m-1)2.
(1)证明:由题意得,△=(3m+1)2-4m(2m+2)=(m-1)2.
∵m>1,
∴△=(m-1)2>0.
∴方程有两个不等实根.
(2)由题意得,$x=\frac{{3m+1±\sqrt{{{({m-1})}^2}}}}{2m}=\frac{{3m+1±({m-1})}}{2m}$.
∵m>1,x1>x2,
∴${x_1}=2,{x_2}=1+\frac{1}{m}$.
∴$y=m({1+\frac{1}{m}})-4=m-3$.
(3)根据题意新的函数为:y=$\left\{\begin{array}{l}{m-3,(m>2)}\\{-m+1,(m>2)}\end{array}\right.$
解$\left\{\begin{array}{l}{y=2m+b}\\{y=-m+1}\end{array}\right.$得$\left\{\begin{array}{l}{m=\frac{1-b}{3}}\\{y=\frac{2+b}{3}}\end{array}\right.$,
函数y=2m+b的图象与此图象有两个公共点时,则$\left\{\begin{array}{l}{\frac{1-b}{3}>2}\\{\frac{2+b}{3}<-1}\end{array}\right.$,
解得b<-5.
故答案为b<-5.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.同时考查了解一元一次方程和解不等式组.

 金状元绩优好卷系列答案
金状元绩优好卷系列答案| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 |
| 2012年3月 | 3℃ | 5℃ | 3℃ | 5℃ | 6℃ | 8℃ |
| 2013年3月 | 6℃ | 6℃ | 11℃ | 14℃ | 15℃ | 14℃ |
(2)利用(1)的结果,你来分析一下,2012年3月1日~6日和2013年3月1日~6日相比,哪个时间段的气温相对较高?哪个时间段的气温相对较稳定?
| A. | x2•x3=x6 | B. | (x2)3=x5 | C. | x5÷x3=x2 | D. | x2+x3=2x5 |
| A. | a6÷a3=a3 | B. | a2•a3=a6 | C. | (a2b)3=a6b | D. | ($\frac{a}{b}$)3=$\frac{{a}^{3}}{b}$ |