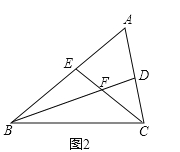
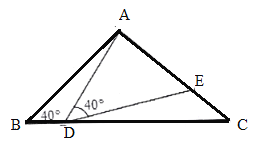
题目内容
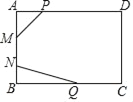
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动(
上运动(![]() 不与
不与![]() 、
、![]() 重合),连接
重合),连接![]() ,作
,作![]() ,
,![]() 交线段
交线段![]() 于
于![]() .
.
(1)当![]() 时,
时,![]() ______________
______________![]() ;点
;点![]() 从
从![]() 向
向![]() 运动时,
运动时,![]() 逐渐变____________(填“大”或“小”);
逐渐变____________(填“大”或“小”);
(2)当![]() 时,求证:
时,求证:![]() ,请说明理由;
,请说明理由;
(3)在点![]() 的运动过程中,
的运动过程中,![]() 的形状也在改变,判断当
的形状也在改变,判断当![]() 等于多少度时,
等于多少度时,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)25°;小;(2)见解析;(3)当∠BDA的度数为80°或110°时,△ADE是等腰三角形.
【解析】
(1)利用三角形内角和定理,即可求出![]() ;然后根据∠BAD的变化情况,即可判断
;然后根据∠BAD的变化情况,即可判断![]() 的变化情况;
的变化情况;
(2)利用∠DEC+∠EDC=140°,∠ADB+∠EDC=140°,求出∠ADB=∠DEC,再利用AAS即可得出△ABD≌△DCE;
(3)根据等腰三角形的腰的情况分类讨论,再利用等腰三角形的性质和三角形的外角即可分别求出∠BDA.
解:∵在△BAD中,∠B=40°,∠BDA=115°,
∴∠BAD=180°﹣∠B﹣∠BDA=25°;
∠BAD+∠BDA=180°﹣∠B=140°
由图可知:点![]() 从
从![]() 向
向![]() 运动时,∠BAD逐渐变大,则
运动时,∠BAD逐渐变大,则![]() 逐渐变小.
逐渐变小.
故答案为:25°;小;
(2)∵∠B=∠C=40°,
∴∠DEC+∠EDC=180°﹣∠C=140°,
又∵∠ADE=40°,
∴∠ADB+∠EDC=180°﹣∠ADE =140°,
∴∠ADB=∠DEC,
∵![]() ,
,![]()
∴![]()
在△ABD和△DCE中,

∴△ABD≌△DCE(AAS).
(3)当△ADE是等腰三角形时,∠BDA的度数为80°或110°,
①当ED=EA时,
∴∠DAE=∠EDA=40°,
∴∠BDA=∠C+DAE=80°;
②当DA=DE时,
∴∠DAE=∠DEA=![]() (180°﹣∠ADE)=70°,
(180°﹣∠ADE)=70°,
∴∠BDA=∠C+DAE=110°,
③当AD=AE时,
∠ADE=∠AED=40°
∵∠C=40°
∠AED是△EDC的外角
∴∠AED>∠C,与∠AED=40°矛盾
所以此时不成立;
综上所述:当∠BDA的度数为80°或110°时,△ADE是等腰三角形.