题目内容
1.设x1,x2是方程x2+x-4=0的两个实数根,求代数式x12-5x22+10的值.分析 先利用一元二次方程解的定义得到x12=-x1+4,x22=-x2+4,则x12-5x22+10=-x1+5x2-6,再利用根与系数的关系得到x1=-x2-1,所以原式=6x2-5,然后解方程x2+x-4=0,把x的值代入原式=6x2-5中计算即可.
解答 解:∵x1,x2是方程x2+x-4=0的两个实数根,
∴x12+x1-4=0,x22+x2-4=0,
即x12=-x1+4,x22=-x2+4,
∴x12-5x22+10=-x1+4-5(-x2+4)+10
=-x1+5x2-6,
∵x1,x2是方程x2+x-4=0的两个实数根,
∴x1+x2=-1,
∴x1=-x2-1,
∴原式=x2+1+5x2-6
=6x2-5,
解方程x2+x-4=0得x=$\frac{-1±\sqrt{17}}{2}$,
∴原式=3(-1+$\sqrt{17}$)-5=-8+3$\sqrt{17}$或原式=3(-1-$\sqrt{17}$)-5=-8-3$\sqrt{17}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.下列式子中,属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{\frac{1}{3}}$ |
12. 如图,AB∥CD,∠AFE=α,∠DCE=β,则∠E为( )
如图,AB∥CD,∠AFE=α,∠DCE=β,则∠E为( )
 如图,AB∥CD,∠AFE=α,∠DCE=β,则∠E为( )
如图,AB∥CD,∠AFE=α,∠DCE=β,则∠E为( )| A. | β-α | B. | α+β-180° | C. | β-2α | D. | 180°-α-β |
9.下列命题是真命题的是( )
| A. | 邻补角相等 | B. | 对顶角相等 | C. | 内错角相等 | D. | 同位角相等 |
16. 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
 如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )
如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )| A. | (1,-1) | B. | (2,0) | C. | (-1,1) | D. | (-1,-1) |
6.下列命题中,为真命题的是( )
| A. | 如果-2x>-2,那么x>1 | B. | 如果a2=b2,那么a3=b3 | ||
| C. | 面积相等的三角形全等 | D. | 如果a∥b,b∥c,那么a∥c |
10.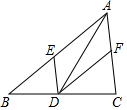 在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )
在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )
 在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )
在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD⊥BC,那么四边形AEDF是菱形 | |
| D. | 如果AD平分∠BAC,那么四边形AEDF是菱形 |