题目内容
11.在直角三角形ABC中,∠C=90°,CA=CB=1,点P是边AC一动点,点Q在边CB的延长线上,且AP=BQ,连接PQ交线段AB于点O.(Ⅰ)如图1,小丁过点P作PH∥CB交线段AB于H,发现△OPH≌△OQB,请证明小丁发现的结论.
(Ⅱ)如图2,过点O作OM,ON分别垂直于AC,BC于点M,N,若四边形OMCN的面积为$\frac{2}{9}$,求线段CP的长度.
(Ⅲ)如图3,点P关于直线AB的对称点为P′,连接OP′,CP′,试说明∠OP′C=45°.
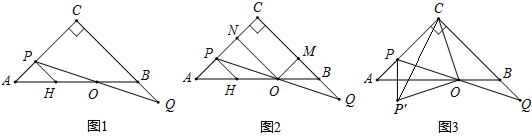
分析 (1)易证∠OPH=∠Q,即可证明△OPH≌△OQB;
(2)易证ON=AN,OM=CN,即可求得CN、AN的值,易证OB=OH,根据平行线性质可得CN=PN,即可解题;
(3)过C作CG⊥AB,作PH∥BC,易证OP=OQ,OH=OB,HK=AK,即可求得OK=CG,即可证明RT△OP'K≌RT△COG,可得∠P′OK=∠OCG,即可求得∠P′OK+∠COG=90°,即可解题.
解答 (1)证明:∵PH∥BC,
∴∠OPH=∠Q,
在△OPH和△OQB中,
$\left\{\begin{array}{l}{∠BOQ=∠HOP}\\{∠OPH=∠Q}\\{PH=BQ}\end{array}\right.$,
∴△OPH≌△OQB(AAS);
(2)解:∵ON⊥AC,∠A=45°,
∴ON=AN,
∵ON⊥AC,OM⊥BC,∠C=90°,
∴四边形OMCN为矩形,
∴OM=CN,
∵CN•NO=$\frac{2}{9}$,CN+NO=1,
∴CN=$\frac{1}{3}$,AN=$\frac{2}{3}$,
∵△OPH≌△OQB,
∴OB=OH,
∵PH∥BC,
∴$\frac{HO}{BO}$=$\frac{PN}{CN}$=1,
∴CP=$\frac{2}{3}$;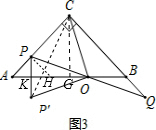
(3)解:过C作CG⊥AB,作PH∥BC,
∵点P关于直线AB的对称点为P′,
∴OP=OP′,
∵△OPH≌△OQB,
∴OP=OQ,OH=OB,
∵PH∥BC,
∴△APH为等腰直角三角形,
∵PP′⊥AH,
∴HK=AK,
∴OK=$\frac{1}{2}$AB,
∵CG⊥AB,
∴CG=AO=BO=$\frac{1}{2}$AB,
∴OK=CG,
在Rt△OP′K和Rt△COG中,
$\left\{\begin{array}{l}{OK=CG}\\{OC=OP′}\end{array}\right.$,
∴Rt△OP′K≌Rt△COG(HL),
∴∠P′OK=∠OCG,OC=OP′,
∵∠OCG+∠COG=90°,
∴∠P′OK+∠COG=90°,即∠P′OC=90°,
∴△COP′是等腰直角三角形,
∴∠CP′O=45°.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△OPH≌△OQB和RT△OP'K≌RT△COG是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
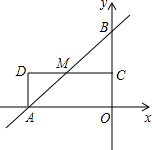 如图,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
如图,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形. 如图,AC是?ABCD的对角线,E是AC上一点,且CE=2AE,问:在线段EC上是否存在一点F,使四边形BFDE是平行四边形?若存在,请确定点F的位置,并证明你的结论;若不存在,请说明理由.
如图,AC是?ABCD的对角线,E是AC上一点,且CE=2AE,问:在线段EC上是否存在一点F,使四边形BFDE是平行四边形?若存在,请确定点F的位置,并证明你的结论;若不存在,请说明理由.
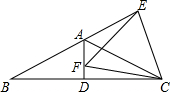 如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点E是BA延长线上一点,点F是线段AD上一点,FE=FC.下列结论:
如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点E是BA延长线上一点,点F是线段AD上一点,FE=FC.下列结论: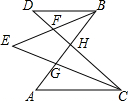 如图,已知BE平分∠DBA交DC于F,CE平分∠DCA交AB于G,AB和CD交于H,∠A=45°,∠D=45°,求∠E的度数.
如图,已知BE平分∠DBA交DC于F,CE平分∠DCA交AB于G,AB和CD交于H,∠A=45°,∠D=45°,求∠E的度数.