题目内容
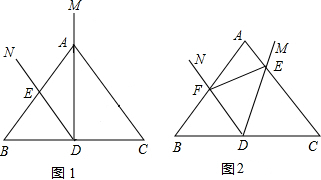
20. 如图,已知BE平分∠DBA交DC于F,CE平分∠DCA交AB于G,AB和CD交于H,∠A=45°,∠D=45°,求∠E的度数.
如图,已知BE平分∠DBA交DC于F,CE平分∠DCA交AB于G,AB和CD交于H,∠A=45°,∠D=45°,求∠E的度数.
分析 先根据角平分线定义得到∠1=∠2,∠3=∠4,再利用三角形内角和定理和对顶角相等得到∠1+∠D=∠4+∠E①,∠1+∠2+∠D=∠3+∠4+∠A,即2∠1+∠D=2∠4+∠A②,接着利用①×2-②得∠E=$\frac{1}{2}$(∠D+∠A),然后把∠A=45°,∠D=45°代入计算即可.
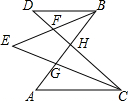
解答 解:如图,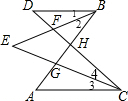
∵BE平分∠DBA交DC于F,CE平分∠DCA交AB于G,
∴∠1=∠2,∠3=∠4,
∵∠1+∠D=∠4+∠E①,
∠1+∠2+∠D=∠3+∠4+∠A,即2∠1+∠D=2∠4+∠A②,
由①×2-②得∠D=2∠E-∠A,
∴∠E=$\frac{1}{2}$(∠D+∠A)=$\frac{1}{2}$×(45°+45°)=45°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.解答的关键是找准相关的三角形,然后利用三角形内角和定理建立等量关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.下列各式成立的是( )
| A. | 2<$\sqrt{7}$<3 | B. | (2+5)2=22+52 | C. | m(m+b)=m2+b | D. | 2$\sqrt{2}$-$\sqrt{2}$=2 |
12. 如图是某几何体的三视图,则该几何体是( )
如图是某几何体的三视图,则该几何体是( )
 如图是某几何体的三视图,则该几何体是( )
如图是某几何体的三视图,则该几何体是( )| A. | 正方体 | B. | 圆锥体 | C. | 圆柱体 | D. | 球体 |
10.如果a>b,那么下列不等式一定成立的是( )
| A. | a-b<0 | B. | -a>-b | C. | $\frac{1}{2}$a<$\frac{1}{2}$b | D. | 2a>2b |