题目内容
19.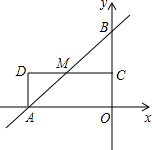 如图,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
如图,直线y=$\frac{4}{3}$x+8分别交x轴,y轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.(1)求证:AB、CD互相平分.
(2)动点P从A出发,以每秒2个单位长度的速度,沿AO、OC向点C作匀速运动,设点P运动的时间为t秒,在动点P从A出发的同时,动点Q从C出发,以每秒1个单位长度的速度,沿CM向点M作匀速运动,当P,Q中的一点到达终点后,该点停止运动,另一点继续运动,直至到达终点,整个运动停止,问:是否存在这样的t,使得直线PQ将四边形AOCM的面积分成1:3两部分?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
分析 (1)先求出点A、B的坐标,由C为OB的中点,得出M为AB的中点,再求出CM为△OAB的中位线,得出CM=$\frac{1}{2}$OA=$\frac{1}{2}$CD=3,M为CD的中点,即可得出结论;
(2)分三种情况:①当0<t<3时,由题意得出关于t的方程,解方程即可;
②当t=3时,由△MOC的面积=$\frac{1}{2}$×3×4=6≠18×$\frac{1}{4}$,得出t≠3;
③当3<t≤5时,Q停止运动,OP=2t-6,得出CP=10-2t,由△MCP的面积=$\frac{1}{2}$×3×(10-2t)=$\frac{1}{4}$×18,解方程即可.
解答 (1)证明:对于直线y=$\frac{4}{3}$x+8,
当x=0时,y=8;当y=0时,x=-6;
∴A(-6,0),B(0,8),OA=6,OB=8,
∵四边形AOCD是矩形,
∴OA∥CD,CD=OA=6,
∵点C为OB的中点,
∴M为AB的中点,
∴CM为△OAB的中位线,
∴CM=$\frac{1}{2}$OA=$\frac{1}{2}$CD=3,
∴M为CD的中点,
∴AB、CD互相平分;
(2)解:存在;
梯形AOCM的面积=$\frac{1}{2}$(3+6)×4=18;
分三种情况讨论:
①当0<t<3时,如图1所示: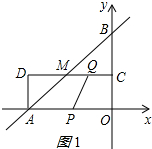 若梯形APQM的面积=$\frac{1}{2}$(2t+3-t)×4=18×$\frac{1}{4}$,
若梯形APQM的面积=$\frac{1}{2}$(2t+3-t)×4=18×$\frac{1}{4}$,
解得:t=-$\frac{3}{4}$,不合题意,舍去;
若梯形APQM的面积=$\frac{1}{2}$(2t+3-t)×4=18×$\frac{3}{4}$,
解得:t=$\frac{15}{4}$,不合题意,舍去;
②当t=3时,∵△MOC的面积=$\frac{1}{2}$×3×4=6≠18×$\frac{1}{4}$,
∴t≠3;
③当3<t≤5时,如图2所示: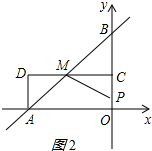
Q停止运动,OP=2t-6,
∴CP=4-(2t-6)=10-2t,
当△MCP的面积=$\frac{1}{2}$×3×(10-2t)=$\frac{1}{4}$×18时,
解得:t=$\frac{7}{2}$,符合题意;
综上所述:当t=$\frac{7}{2}$时,直线PQ将四边形AOCM的面积分成1:3两部分.
点评 本题是一次函数综合题,考查了一次函数点的坐标特征、三角形中位线的性质、梯形面积的计算、三角形面积的计算、解方程等知识;本题难度较大,综合性强,特别是(2)中,需要进行分类讨论,才能得出结果.

| A. | 2<$\sqrt{7}$<3 | B. | (2+5)2=22+52 | C. | m(m+b)=m2+b | D. | 2$\sqrt{2}$-$\sqrt{2}$=2 |
 如图是某几何体的三视图,则该几何体是( )
如图是某几何体的三视图,则该几何体是( )| A. | 正方体 | B. | 圆锥体 | C. | 圆柱体 | D. | 球体 |
 如图所示,与∠1是同位角的个数有2个,并在图中标出.
如图所示,与∠1是同位角的个数有2个,并在图中标出.