题目内容
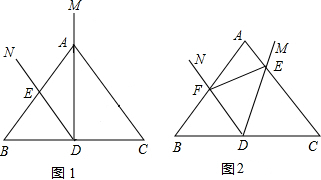
16. 如图,AC是?ABCD的对角线,E是AC上一点,且CE=2AE,问:在线段EC上是否存在一点F,使四边形BFDE是平行四边形?若存在,请确定点F的位置,并证明你的结论;若不存在,请说明理由.
如图,AC是?ABCD的对角线,E是AC上一点,且CE=2AE,问:在线段EC上是否存在一点F,使四边形BFDE是平行四边形?若存在,请确定点F的位置,并证明你的结论;若不存在,请说明理由.
分析 首先连接BD,根据平行四边形的性质可知:AO=CO,BO=DO,再根据条件AE=CF,可得到EO=FO,根据对角线互相平分的四边形是平行四边形可证出结论.
解答  解:存在,如图当CF=AE时,四边形BFDE是平行四边形,
解:存在,如图当CF=AE时,四边形BFDE是平行四边形,
证明:证明:连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,
∵AE=CF,
∴EO=FO,
∴四边形BFDE是平行四边形.
点评 此题主要考查了平行四边形的判定与性质,关键是掌握平行四边形对角线互相平分,对角线互相平分的四边形是平行四边形.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7.下列各式成立的是( )
| A. | 2<$\sqrt{7}$<3 | B. | (2+5)2=22+52 | C. | m(m+b)=m2+b | D. | 2$\sqrt{2}$-$\sqrt{2}$=2 |
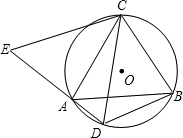 如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.