题目内容
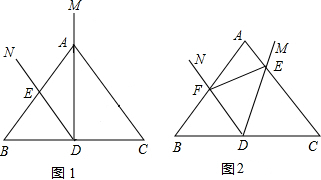
16.如下列各图,Rt△ABC中,∠ACB=90°,分别以AB、BC、CA为边向外作半圆、正三角形、等腰直角三角形等,面积分别为S1、S2、S3.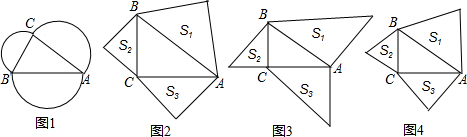
(1)在图1中,S1、S2、S3有什么关系?写出关系式:S2+S3=S1.
(2)探索图2、图3、图4中S1、S2、S3是否有同样的规律?选一个作出证明.
(3)在图4中,若BC=4,AC=5,求S1+S2+S3.
分析 (1)由扇形的面积公式可知S1=$\frac{1}{8}$π•AB2,S2=$\frac{1}{8}$π•BC2,S3=$\frac{1}{8}$π•AC2,在Rt△ABC中,由勾股定理得BC2+AC2=AB2,即S2+S3=S1;
(2)根据(1)中的求解即可得出答案;
(3)利用(2)中的结论进行求解.
解答 解:(1)∵S1=$\frac{1}{8}$π•AB2,S2=$\frac{1}{8}$π•BC2,S3=$\frac{1}{8}$π•AC2,
根据勾股定理可知AB2=BC2+AC2,
∴S2+S3=S1;
(2)图2、图3、图4中S1、S2、S3有同样的规律:S2+S3=S1.
如图3,∵S1=$\frac{1}{2}$AB2,S2=$\frac{1}{2}$BC2,S3=$\frac{1}{2}$AC2,
根据勾股定理可知AB2=BC2+AC2,
∴S2+S3=S1;
(3)如图4,∵三个三角形都是正三角形,
∴S2=$\frac{1}{2}$×4×(4×$\frac{\sqrt{3}}{2}$)=4$\sqrt{3}$,
S3=$\frac{1}{2}$×5×(5×$\frac{\sqrt{3}}{2}$)=$\frac{25}{4}$$\sqrt{3}$,
∴S1=4$\sqrt{3}$+$\frac{25}{4}$$\sqrt{3}$=$\frac{41}{4}$$\sqrt{3}$,
∴S1+S2+S3=$\frac{41}{4}$$\sqrt{3}$+4$\sqrt{3}$+$\frac{25}{4}$$\sqrt{3}$=$\frac{41}{2}$$\sqrt{3}$.
故答案为:S2+S3=S1.
点评 该题主要考查了勾股定理及其应用问题;解题的关键是灵活运用勾股定理等几何知识点来分析、判断、推理或解答.

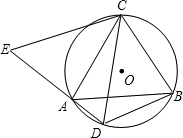 如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=kx上,则(1)k=$\frac{\sqrt{3}}{3}$,(2)A2015的坐标是(2015$\sqrt{3}$,2017).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y=kx上,则(1)k=$\frac{\sqrt{3}}{3}$,(2)A2015的坐标是(2015$\sqrt{3}$,2017).