题目内容
13. 如图是半径为2的圆.
如图是半径为2的圆.(1)在其中画两个不重叠的扇形AOB和扇形BOC,使扇形AOB的圆心角为120°,扇形BOC的圆心角为90°;
(2)求第三个扇形AOC的面积.
分析 (1)根据扇形定义及题目要求画出即可;
(2)根据扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$计算即可.
解答 解:(1)如图所示:
(2)∵∠AOB=120°,∠BOC=90°,
∴∠AOC=150°,
故S扇形AOC=$\frac{150×π×{2}^{2}}{360}$=$\frac{5}{3}$π.
点评 本题考查的是扇形面积的计算,根据题意求出对应圆心角度数是前提,掌握扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$是解题的关键.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 经过两点可以画无数条直线 | |
| B. | 两条射线组成的图形叫做角 | |
| C. | 正多边形的各边都相等,各角都相等 | |
| D. | 两个锐角的和一定大于直角 |
18.线段CD是由线段AB平移得到的,点A(-1,4)的对应点为C(-1,7),则点B(-4,-1)的对应点D的坐标为( )
| A. | (2,9) | B. | (5,3) | C. | (-4,2) | D. | (-9,-4) |
3.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是$\frac{5}{2}$;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
| A. | ①②③ | B. | ②③④ | C. | ②③ | D. | ①④ |
 如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c.
如图,在Rt△ABC中,∠C=90°,∠A=30°,a=5,求∠B,b,c.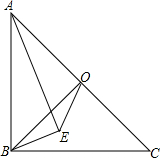 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证: