题目内容
17.已知在平面直角坐标系中,一次函数y=$\frac{3}{4}$x+3的图象与y轴交于点A,点M在正比例函数y=$\frac{3}{2}$x的图象x>0的那部分上,且MO=MA(O为坐标原点).(1)求线段AM的长;
(2)若反比例函数y=$\frac{k}{x}$的图象经过点M关于y轴的对称点M′,求反比例函数解析式,并直接写出当x>0时,$\frac{3}{4}$x+3与$\frac{k}{x}$的大小关系.
分析 (1)求出点A为(0,3),设M的坐标为(m,$\frac{3}{2}$m),根据勾股定理求出MA2与MO2,列出方程求出m的值即可.
(2)求出M′的坐标,求出反比例函数的解析式,然后求出两图象的交点坐标后即可判断$\frac{3}{4}$x+3与$\frac{k}{x}$的大小关系
解答 解:(1)令x=0代入y=$\frac{3}{4}$x+3中,
∴y=3,
∴A(0,3)
设M(m,$\frac{3}{2}$m),其中m>0,
∴由勾股定理可知:MO2=m2+$\frac{9}{4}$m2=$\frac{13}{4}$m2,
MA2=m2+($\frac{3}{2}$m-3)2,
∵MA=MO,
∴$\frac{13}{4}$m2=m2+($\frac{3}{2}$m-3)2,
∴m=1,
∴M(1,$\frac{3}{2}$),
由勾股定理可知:AM=$\sqrt{{1}^{2}+(\frac{3}{2}-3)^{2}}$=$\frac{\sqrt{13}}{2}$
(2)由题意可知:M′(-1,$\frac{3}{2}$)
将M′(-1,$\frac{3}{2}$)代入y=$\frac{k}{x}$
∴k=-$\frac{3}{2}$
∴联立$\left\{\begin{array}{l}{y=-\frac{3}{2x}}\\{y=\frac{3}{4}x+3}\end{array}\right.$
解得:x=-2$±\sqrt{2}$
当x>0时,$\frac{3}{4}$x+3>-$\frac{3}{2x}$
点评 本题考查一次函数与反比例函数的综合问题,解题的关键是根据勾股定理求出M的坐标,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.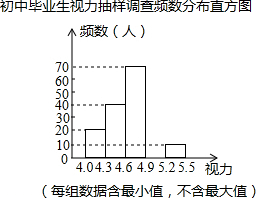 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
(1)本次调查的样本容量为200;
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?
 某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:
某区对即将参加中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图,请根据图表信息回答下列问题:初中毕业生视力抽样调查频数分布表
| 视力 | 频数(人) | 频率 |
| 4.0≤x<4.3 | 20 | 0.1 |
| 4.3≤x<4.6 | 40 | 0.2 |
| 4.6≤x<4.9 | 70 | 0.35 |
| 4.9≤x<5.2 | a | 0.3 |
| 5.2≤x<5.5 | 10 | b |
(2)在频数分布表中,a=60,b=0.05,并将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,根据上述信息估计全区初中毕业生中视力正常的学生有多少人?