题目内容
16.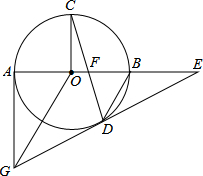 如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.
如图所示,AB是⊙O的直径,OC⊥AB,弦CD与OB交于点F,过圆心O作OG∥BD,交过点A所作⊙O的切线于点G,连结GD并延长与AB的延长线交于点E.(1)求证:GD是⊙O的切线;
(2)试判断△DEF的形状,并说明理由;
(3)若OF:OB=1:3,⊙O的半径为3,求AG的长.
分析 (1)连结OD,如图,由AG是过点A的切线,AB是⊙O的直径,得到∠GAB=90°,由于OG∥BD,得到∠AOG=∠OBD,∠DOG=∠ODB.由等量代换得到∠AOG=∠DOG,证得△AOG≌△DOG,得到OD⊥DE即可证得GD是⊙O的切线;
(2)由(1)知,OD⊥DE,即∠ODC+∠EDF=90°,由OC=OD,得到∠C=∠ODC,∠EDF+∠C=90°,而OC⊥OB,证得∠EDF=∠DFE,即可得到结果
(3)在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,由于OD2+DE2=OE2,得到∴DE=4,OE=5,根据AG为⊙O的切线,得到∠GAE=90°,而∠OED=∠GEA,推出Rt△EOD∽Rt△EGA,得到比例式即可得到结果.
解答 (1)证明:连结OD,如图,
∵AG是过点A的切线,AB是⊙O的直径,
∴AG⊥AB,
∴∠GAB=90°,
∵OG∥BD,
∴∠AOG=∠OBD,∠DOG=∠ODB.
∵OC=OB,
∴∠OBD=∠ODB,
∴∠AOG=∠DOG,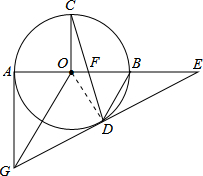
在△AOG和△DOG中,
$\left\{\begin{array}{l}{OA=OD}\\{∠AOG=∠DOG}\\{OG=OG}\end{array}\right.$,
∴△AOG≌△DOG,
∴∠ODG=∠GAB=90°,即OD⊥DE
∵OD是⊙O的半径,
∴GD是⊙O的切线;
(2)解:△DEF是等腰三角形.理由如下:
由(1)知,OD⊥DE,
∴∠ODE=90°,即∠ODC+∠EDF=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠EDF+∠C=90°,
而OC⊥OB,
∴∠C+∠OFC=90°,
∴∠OFC=∠EDF,
∵∠DFE=∠OFC,
∴∠EDF=∠DFE,
∴DE=EF,
∴△DEF是等腰三角形;
(3)解:∵OF:OB=1:3,⊙O的半径为3,
∴OF=1,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=OE2,
∴32+x2=(x+1)2,
解得x=4,
∵DE=EF,
∴DE=4,OE=5,
∵AG为⊙O的切线,
∴AG⊥AE,
∴∠GAE=90°,
而∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴$\frac{OD}{AG}=\frac{DE}{AE}$,即$\frac{3}{AG}=\frac{4}{3+5}$,
∴AG=6.
点评 本题考查了切线的判定和性质,全等三角形的判定与性质,相似三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
| A. | x与y都是变量,且x是自变量,y是因变量 | |
| B. | 所挂物体质量为4kg时,弹簧长度为12cm | |
| C. | 弹簧不挂重物时的长度为0cm | |
| D. | 物体质量每增加1kg,弹簧长度y增加0.5cm |
| A. | 3排5座 | B. | 5排3座 | C. | 5排5座 | D. | 3排3座 |
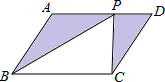 如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )
如图,P是?ABCD上一点.已知S△ABP=3,S△PDC=2,那么平行四边形ABCD的面积是( )| A. | 6 | B. | 8 | C. | 10 | D. | 无法确定 |
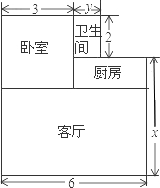 老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示.
老李购买了一套学位房,他准备将地面铺上地砖,地面结构如图所示. 请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.
请采用两种不同的方法,在如图的方格纸中画出两条互相垂直的直线.