题目内容
6.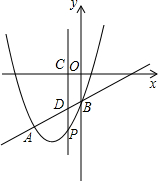 如图,抛物线y=ax2+4x+c(a≠0)与直线y=x-1交于A、B两点,点A的横坐标为-3,B在y轴上,P点是第三象限内抛物线上一动点,横坐标为m,过P作PC⊥x轴于C,交直线AB于点D.
如图,抛物线y=ax2+4x+c(a≠0)与直线y=x-1交于A、B两点,点A的横坐标为-3,B在y轴上,P点是第三象限内抛物线上一动点,横坐标为m,过P作PC⊥x轴于C,交直线AB于点D.(1)求a和c;
(2)当△PAD为直角三角形时,求出点P的坐标;
(3)是否存在点P,使S△PBD:S四边形OBDC=1:2?若存在,直接写出P点横坐标m的值;若不存在,请说明理由.
分析 (1)将点A横坐标代入y=x-1,得出点A纵坐标,再将x=0代入y=x-1,得出点B坐标,把点A,B坐标代入抛物线解析式,从而得出a与c的值;
(2)如图2,当∠APD=90°时,设出P点的坐标,就可以表示出D的坐标,由△APD∽△FCD列出比例式求解即可;如图3,当∠PAD=90°时,作AE⊥x轴于E,根据比例式表示出AD,再由△PAD∽△FEA列出比例式求解;
(3)存在点P,使S△PBD:S四边形OBDC=1:2,连结OP,由P点的横坐标为m可以表示出P、D的坐标,由此表示出S四边形OBDC和2S△BPD建立方程求出其解即可.
解答 解:(1)∵点A的横坐标为-3,点A在直线y=x-1上,
∴点A的纵坐标为-4,
∵B在y轴上,
∴点B的坐标为(0,-1),
把点A和点C的坐标分别代入抛物线y=ax2+4x+c(a≠0)得:
$\left\{\begin{array}{l}{-4=9a-12+c}\\{-1=c}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{c=-1}\end{array}\right.$;
(2)如图2,当∠APD=90°时,设P(m,m2+4m-1),则D(m,m-1),
∴AP=m+3,CD=1-m,OC=-m,CP=1-4m-m2,
∴DP=1-4m-m2-1+m=-3m-m2.
在y=x-1中,当y=0时,x=1,
∴F(1,0),
∴OF=1,
∴CF=1-m.AF=4$\sqrt{2}$.
∵PC⊥x轴,
∴∠PCF=90°,
∴∠PCF=∠APD,
∴CF∥AP,
∴△APD∽△FCD,
∴$\frac{AP}{CF}=\frac{DP}{CD}$,
∴$\frac{m+3}{1-m}=\frac{-3m-{m}^{2}}{1-m}$,
解得:m=-1或m=-3(舍去),
∴P(-1,-4)
如图3,当∠PAD=90°时,作AE⊥x轴于E,
∴∠AEF=90°,CE=m+3,EF=4,AF=4$\sqrt{2}$,PD=m-1-(-1+4m+m2)=-3m-m2.
∵PC⊥x轴,
∴∠DCF=90°,
∴∠DCF=∠AEF,
∴AE∥CD,
∴$\frac{4}{3+m}=\frac{4\sqrt{2}}{AD}$,
∴AD=$\sqrt{2}$(3+m).
∵△PAD∽△FEA,
∴$\frac{PD}{FA}$=$\frac{AD}{AE}$,
$\frac{-3m-{m}^{2}}{4\sqrt{2}}=\frac{\sqrt{2}(3+m)}{4}$,
∴m=-2或m=-3(舍去),
∴P(-2,-5),
当∠APD=90°时,
∴点A与点P关于对称轴对称
∵A(-3,-4)
∴P(-1,-4)
综上,存在点P(-2,-5)或P(-1,-4)使△PAD是直角三角形;
(3)存在点P,使S△PBD:S四边形OBDC=1:2,理由如下:
∵P点横坐标是m(m<0),
∴P(m,m2+4m-1),D(m,m-1),
如图1①,作BE⊥PC于E,
∴BE=-m.
CD=1-m,OB=1,OC=-m,CP=1-4m-m2,
∴PD=1-4m-m2-1+m=-3m-m2,
∴$\frac{-m(1+1-m)}{2}$=2×$\frac{-m(-3m-{m}^{2})}{2}$,
解得:m1=0(舍去),m2=-2,m3=-$\frac{1}{2}$;
如图1②,作BE⊥PC于E,
∴BE=-m.
PD=m2+4m-1+1-m=3m+m2,
∴$\frac{-m(1+1-m)}{2}$=2×$\frac{-m({m}^{2}+3m)}{2}$,
解得:m=0(舍去)或m=$\frac{-7+\sqrt{65}}{4}$(舍去)或m=$\frac{-7-\sqrt{65}}{4}$
∴m=-$\frac{1}{2}$,-2或$\frac{-7-\sqrt{65}}{4}$时,使S△PBD:S四边形OBDC=1:2.
点评 本题考查了待定系数法求二次函数的解析式的运用,四边形的面积公式的运用,三角形的面积公式的运用,相似三角形的判定及性质的运用,解答时函数的解析式是关键,用相似三角形的性质求解是难点.

 阅读快车系列答案
阅读快车系列答案| A. | 绝不可能 | B. | 只是有时可能 | C. | 总是可能 | D. | 只有当P=5时可能 |

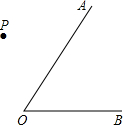 如图,已知点P是∠AOB的外部一点.
如图,已知点P是∠AOB的外部一点.